← Back to Concepts

Ampère's Law

Ampère's Law is one of the four Maxwell equations and provides a powerful method for calculating magnetic fields in situations with high symmetry. It relates the circulation of the magnetic field around a closed loop to the current passing through the loop.

Statement of Ampère's Law

🧲 The Integral Law

Ampère's Law states that the line integral of the magnetic field around a closed path is equal to \( \mu_0 \) times the current passing through the area bounded by the path:

\[ \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} \]

Where:

\( \oint \vec{B} \cdot d\vec{l} \) is the line integral of the magnetic field around a closed path
\( \mu_0 \) is the permeability of free space (4π × 10⁻⁷ T⋅m/A)
\( I_{enc} \) is the total current enclosed by the path

Key Features of Ampère's Law

Symmetry Requirements

High Symmetry: Works best when the current distribution has symmetry
Known Field Direction: Field direction must be predictable from symmetry
Constant Magnitude: Field magnitude should be constant along the integration path
Parallel or Perpendicular: Field should be either parallel or perpendicular to the path

🔬 Symmetry Considerations

Ampère's Law is most effective when:

Cylindrical Symmetry: Long straight wires, coaxial cables
Planar Symmetry: Current sheets, parallel plate conductors
Spherical Symmetry: Spherical current distributions
Translational Symmetry: Infinite current sheets or wires

Advantages Over Biot-Savart

No Integration: Avoids complex vector integrals
Symmetry Exploitation: Uses geometric symmetry to simplify calculations
Direct Calculation: Often gives results directly without intermediate steps
Conceptual Clarity: Emphasizes the relationship between current and field circulation

Applications of Ampère's Law

⚡ Ideal Applications

Ampère's Law is particularly useful for:

Long Straight Wires: Current-carrying conductors with cylindrical symmetry
Coaxial Cables: Concentric cylindrical conductors
Current Sheets: Planar current distributions
Solenoids: Long coils with many turns
Toroids: Ring-shaped solenoids

Example: Magnetic Field of a Long Straight Wire

Problem: Calculate the magnetic field at a distance \( r \) from a long straight wire carrying current \( I \).

Step 1: Choose Amperian Loop

Use a circular path of radius \( r \) centered on the wire:

\[ \oint \vec{B} \cdot d\vec{l} = B(2\pi r) \]

Step 2: Apply Ampère's Law

The enclosed current is \( I \):

\[ B(2\pi r) = \mu_0 I \]

Step 3: Solve for B

The magnetic field is:

\[ B = \frac{\mu_0 I}{2\pi r} \]

Step 4: Direction

The field circulates around the wire according to the right-hand rule.

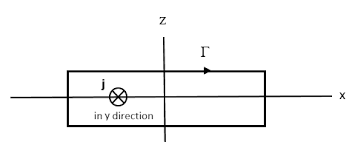
Example: Magnetic Field Inside a Solenoid

Problem: Calculate the magnetic field inside a long solenoid with \( n \) turns per unit length carrying current \( I \).

Step 1: Choose Amperian Loop

Use a rectangular loop with one side inside the solenoid:

\[ \oint \vec{B} \cdot d\vec{l} = BL \]

Step 2: Calculate Enclosed Current

The enclosed current is \( nLI \):

\[ BL = \mu_0 nLI \]

Step 3: Solve for B

The magnetic field inside is:

\[ B = \mu_0 nI \]

Limitations and Considerations

⚠️ Important Limitations

Symmetry Required: Only works for highly symmetric current distributions
Steady Currents: Applies only to steady (DC) currents
Field Direction: Requires knowledge of field direction from symmetry
Complex Geometries: Not suitable for arbitrary current distributions
Displacement Current: Original form doesn't include time-varying electric fields

Relationship to Other Laws

Connection to Biot-Savart Law

Consistency: Both laws give the same results for the same problems
Different Approaches: Ampère's Law uses symmetry, Biot-Savart uses direct integration
Complementary: Each is better suited for different problem types

Quick Quiz: Ampère's Law

1. What does Ampère's Law relate?

Magnetic field circulation to enclosed current

Electric field to charge

Force to acceleration

Energy to power

2. When is Ampère's Law most useful?

For arbitrary current distributions

For symmetric current distributions

For time-varying currents

For magnetic materials only

3. What type of integration does Ampère's Law use?

Line integral around a closed path

Surface integral over an area

Volume integral over a region

Point evaluation at a specific location

Key Takeaways

Symmetry-Based: Ampère's Law works best with symmetric current distributions
Circulation Concept: Relates magnetic field circulation to enclosed current
Powerful Tool: Often simpler than Biot-Savart for symmetric cases
Maxwell Equation: One of the four fundamental equations of electromagnetism
Complementary: Works well with Biot-Savart Law for different problem types