← Back to Concepts

The Biot-Savart Law

The Biot-Savart Law is a fundamental principle in electromagnetism that allows us to calculate the magnetic field produced by a current-carrying wire or any distribution of moving charges. It is the magnetic equivalent of Coulomb's Law for electric fields.

Statement of the Biot-Savart Law

🧲 The Fundamental Law

The Biot-Savart Law states that the magnetic field \( \vec{B} \) at a point due to a current element \( I \, d\vec{l} \) is:

\[ \vec{B} = \frac{\mu_0}{4\pi} \int \frac{I \, d\vec{l} \times \hat{r}}{r^2} \]

Where:

\( \vec{B} \) is the magnetic field vector
\( \mu_0 \) is the permeability of free space (4π × 10⁻⁷ T⋅m/A)
\( I \) is the current
\( d\vec{l} \) is the infinitesimal length element of the wire
\( \hat{r} \) is the unit vector from the current element to the point
\( r \) is the distance from the current element to the point

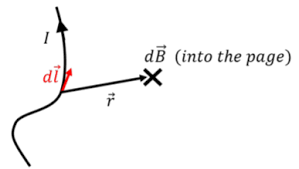
Key Features of the Biot-Savart Law

Vector Nature

Cross Product: The field direction is perpendicular to both \( d\vec{l} \) and \( \hat{r} \)
Right-Hand Rule: Use the right-hand rule to determine field direction
Superposition: Total field is the vector sum of contributions from all current elements

Distance Dependence

Inverse Square: Field strength decreases as \( \frac{1}{r^2} \)
Direction: Field is perpendicular to the line connecting current element and point
Symmetry: Field lines form circles around straight current-carrying wires

🔬 Physical Interpretation

The Biot-Savart Law can be understood as:

Moving Charges: Each moving charge in the current creates a magnetic field
Field Addition: The total field is the sum of all individual charge contributions
Relativistic Effect: Magnetic fields arise from the relativistic transformation of electric fields
Consistency: The law is consistent with Ampère's Law and Maxwell's equations

Applications of the Biot-Savart Law

⚡ Common Applications

The Biot-Savart Law is used to calculate magnetic fields for:

Straight Wires: Long current-carrying conductors
Current Loops: Circular and rectangular current loops
Coils: Multiple-turn coils and solenoids
Complex Geometries: Any current distribution with known geometry

Example: Magnetic Field of a Straight Wire

Problem: Calculate the magnetic field at a distance \( r \) from a long straight wire carrying current \( I \).

Step 1: Use Biot-Savart Law

For a current element \( d\vec{l} \) at position \( z \):

\[ d\vec{B} = \frac{\mu_0 I}{4\pi} \frac{d\vec{l} \times \hat{r}}{r^2} \]

Step 2: Geometry Setup

At distance \( r \) from the wire, the field contribution is:

\[ dB = \frac{\mu_0 I}{4\pi} \frac{dz \sin\theta}{R^2} \]

Where \( R = \sqrt{r^2 + z^2} \) and \( \sin\theta = \frac{r}{R} \).

Step 3: Simplify the Integral

Substituting \( \sin\theta = \frac{r}{R} \):

\[ B = \frac{\mu_0 I r}{4\pi} \int_{-\infty}^{\infty} \frac{dz}{(r^2 + z^2)^{3/2}} \]

Step 4: Evaluate the Integral

Using the standard integral \( \int_{-\infty}^{\infty} \frac{dz}{(a^2 + z^2)^{3/2}} = \frac{2}{a^2} \):

\[ B = \frac{\mu_0 I r}{4\pi} \cdot \frac{2}{r^2} = \frac{\mu_0 I}{2\pi r} \]

Step 5: Direction

The field circulates around the wire according to the right-hand rule.

Limitations and Considerations

⚠️ Important Limitations

Steady Currents: The law applies to steady (DC) currents
Linear Media: Assumes linear magnetic materials
Classical Limit: Does not include quantum effects
Integration Required: Often requires complex integrals for realistic geometries
Symmetry Needed: Ampère's Law is often easier for symmetric cases

Relationship to Other Laws

Connection to Ampère's Law

Consistency: Biot-Savart Law is consistent with Ampère's Law
Different Approaches: Biot-Savart is direct calculation, Ampère's Law uses symmetry
Complementary: Each law is better suited for different problems

Quick Quiz: Biot-Savart Law

1. What does the Biot-Savart Law calculate?

Magnetic field from current elements

Electric field from charges

Force on moving charges

Energy stored in magnetic fields

2. What is the distance dependence in the Biot-Savart Law?

1/r

1/r²

1/r³

1/r⁴

3. When is the Biot-Savart Law most useful?

For symmetric current distributions

For arbitrary current geometries

For time-varying currents

For magnetic materials only

Key Takeaways

Fundamental Law: Biot-Savart Law is the basic law for calculating magnetic fields from currents
Vector Nature: Uses cross product to determine field direction
Inverse Square: Field strength decreases with distance squared
Integration Required: Often requires complex integrals for realistic problems
Complementary: Works well with Ampère's Law for different problem types