Capacitors in Series and Parallel
Capacitors can be connected in different configurations to achieve desired capacitance values. Understanding series and parallel connections is essential for circuit design and analysis. These configurations follow specific rules that determine the equivalent capacitance of the combination.
Capacitors in Series
Capacitors are connected "in series" when they are connected end-to-end, with the positive plate of one connected to the negative plate of the next. This configuration reduces the total capacitance.
What Does "Series" Mean?
In a series connection, the capacitors are connected in a chain:
Series Connection:
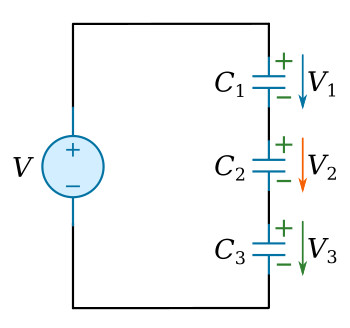
Key Properties of Series Connection
- Same charge: Each capacitor stores the same charge Q
- Voltage (electric potential) adds: Total voltage (electric potential) V = V₁ + V₂ + V₃ + ...
- Current same: Same current flows through all capacitors
- Reduced capacitance: Total capacitance is less than any individual capacitor
Deriving the Series Formula
Let's derive why series capacitors have reduced capacitance:
Derivation:
- Each capacitor has the same charge Q: \(Q_1 = Q_2 = Q_3 = Q\)
- Voltage (electric potential) across each capacitor: \(V_1 = \frac{Q}{C_1}, V_2 = \frac{Q}{C_2}, V_3 = \frac{Q}{C_3}\)
- Total voltage (electric potential): \(V = V_1 + V_2 + V_3 = Q(\frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3})\)
- Equivalent capacitance: \(C_{eq} = \frac{Q}{V} = \frac{Q}{Q(\frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3})}\)
- Result: \(\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}\)
Series Capacitance Formula
$$\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + ...$$
For two capacitors in series:
$$C_{eq} = \frac{C_1 C_2}{C_1 + C_2}$$
This derivation shows why series capacitors have reduced capacitance: the total voltage (electric potential) is the sum of individual voltages (electric potentials), so for the same charge, you need more total voltage (electric potential), meaning less capacitance.
Physical Intuition
Think of series capacitors like resistors in series:
- Charge conservation: The same charge flows through each capacitor
- Voltage (electric potential) division: The total voltage (electric potential) is distributed across all capacitors
- Reduced storage: Less total charge can be stored for a given voltage (electric potential)
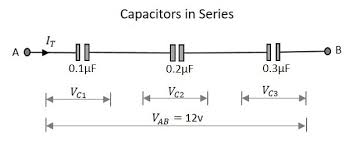
Capacitors in Parallel
Capacitors are connected "in parallel" when all their positive plates are connected together and all their negative plates are connected together. This configuration increases the total capacitance.
What Does "Parallel" Mean?
In a parallel connection, the capacitors are connected side by side:
Parallel Connection:
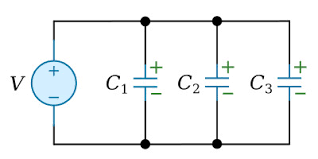
Key Properties of Parallel Connection
- Same voltage (electric potential): Each capacitor has the same voltage (electric potential) V
- Charge adds: Total charge Q = Q₁ + Q₂ + Q₃ + ...
- Current splits: Current divides among the capacitors (not always equally)
- Increased capacitance: Total capacitance is greater than any individual capacitor
Deriving the Parallel Formula
Let's derive why parallel capacitors have increased capacitance:
Derivation:
- Each capacitor has the same voltage (electric potential) V: \(V_1 = V_2 = V_3 = V\)
- Charge on each capacitor: \(Q_1 = C_1V, Q_2 = C_2V, Q_3 = C_3V\)
- Total charge: \(Q = Q_1 + Q_2 + Q_3 = V(C_1 + C_2 + C_3)\)
- Equivalent capacitance: \(C_{eq} = \frac{Q}{V} = \frac{V(C_1 + C_2 + C_3)}{V}\)
- Result: \(C_{eq} = C_1 + C_2 + C_3\)
Parallel Capacitance Formula
$$C_{eq} = C_1 + C_2 + C_3 + ...$$
This derivation shows why parallel capacitors have increased capacitance: the total charge is the sum of individual charges, so for the same voltage (electric potential), you can store more charge, meaning more capacitance.
Physical Intuition
Think of parallel capacitors like resistors in parallel:
- Voltage (electric potential) conservation: All capacitors have the same voltage (electric potential)
- Charge addition: Total charge is the sum of individual charges
- Increased storage: More total charge can be stored for a given voltage (electric potential)
Comparison of Series and Parallel
Key Differences
| Property | Series | Parallel |
|---|---|---|
| Charge | Same on all capacitors | Adds across capacitors |
| Voltage (electric potential) | Adds across capacitors | Same on all capacitors |
| Capacitance | Reduces total capacitance | Increases total capacitance |
| Formula | \(\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2}\) | \(C_{eq} = C_1 + C_2\) |
Worked Examples
Example 1: Capacitors in Series
Problem: Three capacitors of 2.0 μF, 3.0 μF, and 6.0 μF are connected in series. What is the equivalent capacitance?
Solution Steps:
- Given: C₁ = 2.0 μF, C₂ = 3.0 μF, C₃ = 6.0 μF
- Formula: \(\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}\)
- Substitute: \(\frac{1}{C_{eq}} = \frac{1}{2.0} + \frac{1}{3.0} + \frac{1}{6.0}\)
- Calculate: \(\frac{1}{C_{eq}} = 0.5 + 0.333 + 0.167 = 1.0\)
- Result: C_eq = 1.0 μF
Answer: The equivalent capacitance is 1.0 μF.
Example 2: Capacitors in Parallel
Problem: Two capacitors of 4.0 μF and 6.0 μF are connected in parallel. What is the equivalent capacitance?
Solution Steps:
- Given: C₁ = 4.0 μF, C₂ = 6.0 μF
- Formula: C_eq = C₁ + C₂
- Substitute: C_eq = 4.0 + 6.0
- Calculate: C_eq = 10.0 μF
Answer: The equivalent capacitance is 10.0 μF.
Example 3: Mixed Configuration
Problem: Three capacitors of 2.0 μF, 4.0 μF, and 6.0 μF are connected as follows: C₁ and C₂ in parallel, then connected in series with C₃. What is the equivalent capacitance?
Solution Steps:
- Step 1 - Parallel combination: C₁₂ = C₁ + C₂ = 2.0 + 4.0 = 6.0 μF
- Step 2 - Series combination: \(\frac{1}{C_{eq}} = \frac{1}{C_{12}} + \frac{1}{C_3}\)
- Substitute: \(\frac{1}{C_{eq}} = \frac{1}{6.0} + \frac{1}{6.0} = \frac{2}{6.0}\)
- Calculate: C_eq = 3.0 μF
Answer: The equivalent capacitance is 3.0 μF.
Applications and Design Considerations
Series Applications
- Voltage (electric potential) division: Distribute voltage (electric potential) across multiple capacitors
- High-voltage (electric potential) circuits: Use multiple low-voltage (electric potential) capacitors
- Precision timing: Fine-tune capacitance values
- Energy storage: Increase voltage (electric potential) rating while reducing capacitance
Parallel Applications
- Increased capacitance: Achieve higher capacitance values
- Current handling: Distribute current among multiple capacitors
- Redundancy: Improve reliability with backup capacitors
- Filtering: Create effective low-pass filters
Design Considerations
Important Factors
- Voltage (electric potential) ratings: Ensure each capacitor can handle its voltage (electric potential)
- Temperature effects: Capacitance varies with temperature
- Parasitic effects: Consider inductance and resistance
- Manufacturing tolerances: Account for component variations
Common Mistakes to Avoid
⚠️ Common Errors
- Wrong formula: Using series formula for parallel or vice versa
- Mixed configurations: Not simplifying step by step
- Units confusion: Mixing different units (μF, nF, pF)
- Voltage (electric potential) ratings: Forgetting to check voltage (electric potential) limits
- Polarity: Connecting polarized capacitors incorrectly
Practice Problems
Practice Problem 1
Problem: Four capacitors of 1.0 μF each are connected in series. What is the equivalent capacitance?
Click for solution
Solution:
- Given: C₁ = C₂ = C₃ = C₄ = 1.0 μF
- Formula: \(\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \frac{1}{C_4}\)
- Substitute: \(\frac{1}{C_{eq}} = \frac{1}{1.0} + \frac{1}{1.0} + \frac{1}{1.0} + \frac{1}{1.0} = 4\)
- Calculate: C_eq = 0.25 μF
Answer: 0.25 μF
Practice Problem 2
Problem: Three capacitors of 2.0 μF, 3.0 μF, and 5.0 μF are connected in parallel. What is the equivalent capacitance?
Click for solution
Solution:
- Given: C₁ = 2.0 μF, C₂ = 3.0 μF, C₃ = 5.0 μF
- Formula: C_eq = C₁ + C₂ + C₃
- Substitute: C_eq = 2.0 + 3.0 + 5.0
- Calculate: C_eq = 10.0 μF
Answer: 10.0 μF
Practice Problem 3
Problem: Two capacitors of 3.0 μF and 6.0 μF are connected in series, and this combination is connected in parallel with a 2.0 μF capacitor. What is the equivalent capacitance?
Click for solution
Solution:
- Step 1 - Series combination: \(\frac{1}{C_{12}} = \frac{1}{3.0} + \frac{1}{6.0} = \frac{1}{2.0}\)
- Result: C₁₂ = 2.0 μF
- Step 2 - Parallel combination: C_eq = C₁₂ + C₃ = 2.0 + 2.0
- Calculate: C_eq = 4.0 μF
Answer: 4.0 μF
Interactive Simulation
Explore how capacitors behave in series and parallel configurations with this interactive simulation. Adjust the battery voltage and capacitor values to see how the circuit responds.
Circuit Diagram
Circuit Information
Configuration: Series
Battery Voltage (electric potential): 12 V
Total Capacitance: 0.33 μF
Total Charge: 4.0 μC
Controls
Configuration
Battery Settings
Capacitor Values
Circuit Results
How to Use the Simulation
- Configuration: Switch between series and parallel connections
- Battery Voltage: Adjust the power source voltage
- Capacitor Values: Change individual capacitor capacitances
- Calculate: Update the circuit calculations
- Reset: Return to default values
- Show Formulas: Display the mathematical relationships
Key Concepts Summary
- Series connection: Reduces total capacitance, same charge on all capacitors
- Parallel connection: Increases total capacitance, same voltage on all capacitors
- Series formula: \(\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + ...\)
- Parallel formula: \(C_{eq} = C_1 + C_2 + ...\)
- Mixed configurations: Simplify step by step from inside out
- Design considerations: Voltage ratings, temperature effects, parasitic elements
Quick Reference
- Single capacitor: E = ½CV²
- Alternative forms: E = ½QV = Q²/2C
- Series capacitors: E_total = ½C_eqV²
- Parallel capacitors: E_total = ½C_eqV²
- Energy density: Energy per unit mass or volume
- Power: P = dE/dt = VI for time-varying systems
Advanced Capacitor Concepts
Capacitor Networks
Complex capacitor networks can be simplified using systematic approaches:
- Step-by-step reduction: Simplify from inside out
- Symmetry analysis: Use symmetry to simplify calculations
- Delta-Wye transformations: Convert between equivalent configurations
- Superposition: Analyze each source separately
Time-Varying Voltage
When voltage changes with time, capacitors exhibit dynamic behavior:
Instantaneous Current
$$i(t) = C \frac{dV(t)}{dt}$$
Where \(i(t)\) is the instantaneous current and \(V(t)\) is the time-varying voltage.
Instantaneous Power
$$P(t) = V(t) \cdot i(t) = C \cdot V(t) \cdot \frac{dV(t)}{dt}$$
The power delivered to or from the capacitor at any instant.