← Back to Concepts

Circuit Breakdown

Circuit breakdown is a systematic approach to simplify complex circuits by identifying series and parallel combinations, then reducing them step by step to find the equivalent resistance. This method is essential for analyzing complex circuits in AP Physics C.

What is Circuit Breakdown?

Circuit Breakdown: A systematic method to simplify complex circuits by identifying and combining series and parallel resistors step by step until the entire circuit is reduced to a single equivalent resistance.

Circuit breakdown involves:

Step-by-Step Breakdown Method

1
Identify the Circuit Structure
First, carefully examine the circuit to identify all components and their connections. Look for obvious series and parallel combinations.
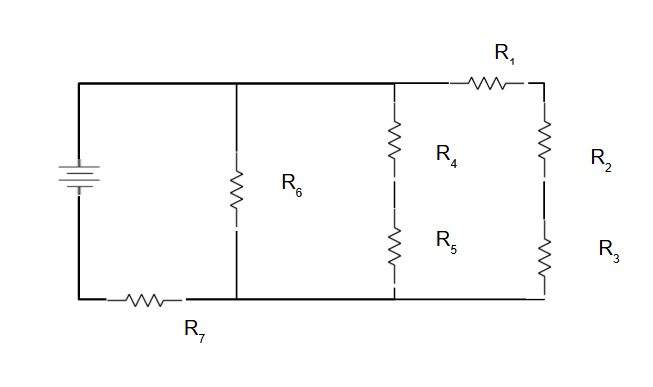
Step 1
💡 Tip: Start by labeling all resistors and identifying which ones are in series vs. parallel.
2
Find Series Combinations
Look for resistors connected end-to-end (series). These can be combined using the series resistance formula.
$$R_{series} = R_1 + R_2 + R_3 + ...$$
Step 2
⚡ Series Rule: Current is the same through all series resistors, voltage divides.
3
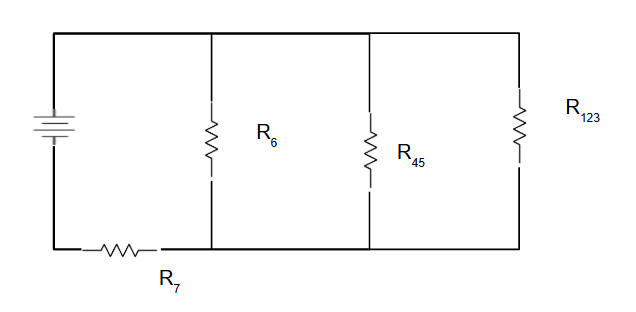
Find Parallel Combinations
Look for resistors connected across the same two points (parallel). These can be combined using the parallel resistance formula.
$$\frac{1}{R_{parallel}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + ...$$
Step 3
⚡ Parallel Rule: Voltage is the same across all parallel resistors, current divides.
4
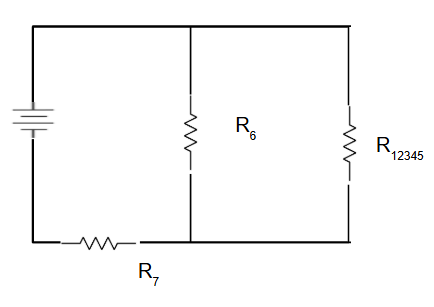
Replace and Redraw
Replace each identified combination with its equivalent resistance and redraw the simplified circuit.
Step 4
🔄 Process: Continue this process until only one equivalent resistor remains.
5
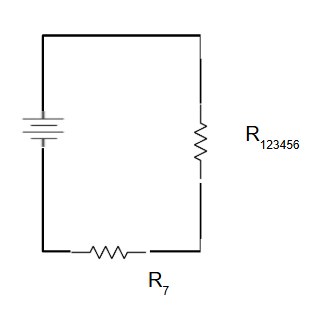
Calculate Final Equivalent Resistance
The final equivalent resistance represents the entire circuit's resistance.
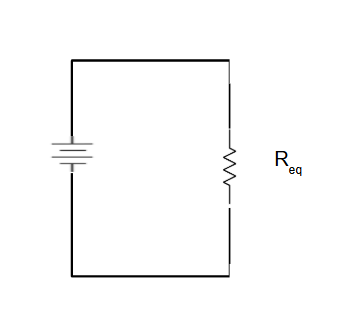
Step 5
✅ Result: This is the total resistance of the original complex circuit.

Some questions will ask you to find the current and voltage across each resistor. To do this, you need to expand (this is taught in the next section).

Worked Example: Complex Circuit

Example: Find the equivalent resistance of the following circuit

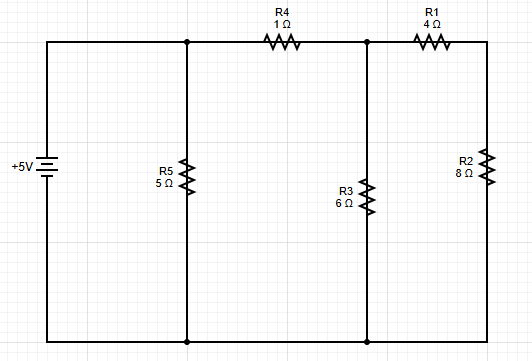
Step 1
Original complex circuit with 5 resistors

Step 1: Combine Series Resistors

Step 2
Circuit after combining R₁ and R₂

R₁ and R₂ are in series:

$$R_{1,2} = R_1 + R_2 = 4Ω + 8Ω = 12Ω$$

Step 2: Combine Parallel Resistors

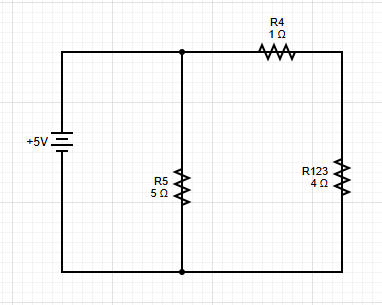
Step 3
Circuit after combining R₁₂ and R₃

R₁₂ and R₃ are in parallel:

$$\frac{1}{R_{1,2,3}} = \frac{1}{R_{1,2}} + \frac{1}{R_3} = \frac{1}{12Ω} + \frac{1}{6Ω}$$ $$R_{1,2,3} = \frac{12Ω}{3} = 4Ω$$

Step 3: Combine Series Resistors

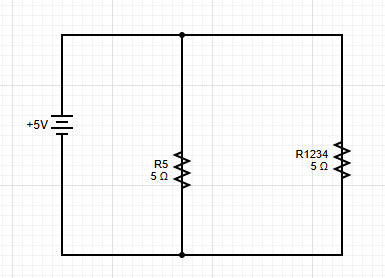
Step 4
Circuit after combining R₁₂₃ and R₄

R₁ and R₂ are in series:

$$R_{1,2,3,4} = R_{1,2,3} + R_4 = 4Ω + 1Ω = 5Ω$$

Step 4: Final Series Combination

Step 5
Final simplified circuit

Now we have three resistors in series:

$$\frac{1}{R_{1,2,3,4,5}} = \frac{1}{R_{1,2,3,4}} + \frac{1}{R_5} = \frac{1}{5Ω} + \frac{1}{5Ω}$$ $$R_{eq} = \frac{5Ω}{2} = 2.5Ω$$

Answer

The equivalent resistance of the circuit is 2.5Ω.

Key Takeaways Summary

🎯 Essential Circuit Breakdown Steps

  1. Identify: Find all series and parallel combinations
  2. Combine Series: Add resistances: R₁ + R₂ + R₃ + ...
  3. Combine Parallel: Use reciprocal formula: 1/R₁ + 1/R₂ + 1/R₃ + ...
  4. Redraw: Replace combinations with equivalent resistors
  5. Repeat: Continue until only one resistor remains

⚡ Key Formulas to Remember

🔍 Identification Rules

✅ Verification Checklist

💡 Pro Tips for Success