Conductors in Electric Fields
Conductors are materials that allow free movement of electrons. When placed in electric fields, conductors exhibit unique behaviors that are fundamental to understanding electrical systems and electrostatic shielding.
What is a Conductor?
Definition
A conductor is a material that contains free electrons that can move easily through the material. Metals like copper, aluminum, and silver are excellent conductors.
In conductors, some electrons are not bound to individual atoms but can move freely throughout the material. This free electron movement is what makes conductors able to carry electric current and respond to electric fields.
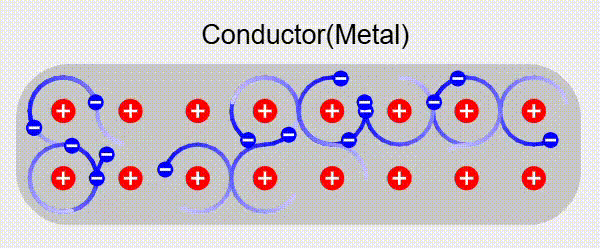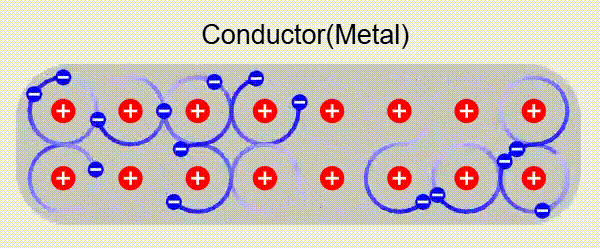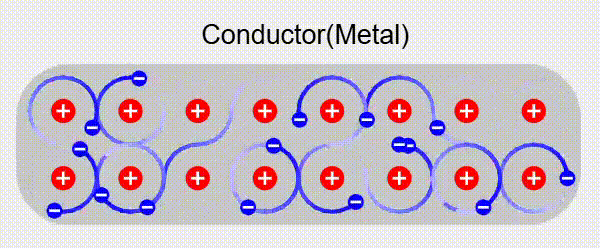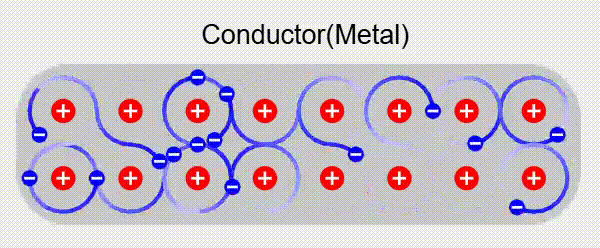
Electrostatic Equilibrium
Key Principle
In electrostatic equilibrium, the electric field inside a conductor is zero:
$$\vec{E}_{\text{inside}} = 0$$
When a conductor is placed in an external electric field, the free electrons redistribute themselves until electrostatic equilibrium is reached. At this point:
- Electric field inside: Zero everywhere inside the conductor
- Electric field at surface: Perpendicular to the surface
- Potential: Constant throughout the conductor
- Charge distribution: Excess charge resides on the surface
Properties of Conductors in Electric Fields
Fundamental Properties
- Zero internal field: Electric field inside conductor is zero
- Surface charge: Excess charge accumulates on the surface
- Equipotential surface: Conductor surface is an equipotential
- Field at surface: Electric field is perpendicular to surface
- Shielding effect: Conductor shields its interior from external fields
Charge Distribution on Conductors
Surface Charge Density
The charge on a conductor's surface is distributed according to the surface curvature:
Where σ is surface charge density, Q is total charge, and A is surface area.
Curvature Effect
Charge density is higher on sharp points and lower on flat surfaces:
- Sharp points: High charge density, strong electric field
- Flat surfaces: Lower charge density, moderate electric field
- Concave regions: Very low charge density, weak electric field

Electric Field at Conductor Surface
Surface Field Formula
The electric field just outside a conductor surface is:
$$E = \frac{\sigma}{\epsilon_0}$$
Where σ is the surface charge density and ε₀ is the permittivity of free space.
This relationship shows that:
- Stronger fields occur where charge density is higher
- Weaker fields occur where charge density is lower
- Field direction is always perpendicular to the surface
- Field magnitude depends only on local charge density
Worked Examples
Example 1: Electric Field Inside a Conductor
Problem: A conducting sphere of radius 5.0 cm has a total charge of +2.0 μC. What is the electric field inside the sphere?
Solution Steps:
- Given: Q = +2.0 × 10⁻⁶ C, r = 5.0 × 10⁻² m
- Property: Electric field inside conductor is zero
- Answer: E = 0 N/C
Answer: The electric field inside the conductor is zero (E = 0 N/C).
Example 2: Surface Charge Density
Problem: A conducting sphere of radius 3.0 cm has a total charge of -1.5 μC. What is the surface charge density?
Solution Steps:
- Given: Q = -1.5 × 10⁻⁶ C, r = 3.0 × 10⁻² m
- Surface area: A = 4πr² = 4π(3.0 × 10⁻²)² = 1.13 × 10⁻² m²
- Surface charge density: σ = Q/A = (-1.5 × 10⁻⁶)/(1.13 × 10⁻²)
- Calculate: σ = -1.33 × 10⁻⁴ C/m²
Answer: The surface charge density is -1.33 × 10⁻⁴ C/m² (negative because the charge is negative).
Example 3: Electric Field at Conductor Surface
Problem: A conducting plate has a surface charge density of +3.0 × 10⁻⁶ C/m². What is the electric field just outside the plate?
Solution Steps:
- Given: σ = +3.0 × 10⁻⁶ C/m², ε₀ = 8.85 × 10⁻¹² C²/N⋅m²
- Formula: E = σ/ε₀
- Substitute: E = (3.0 × 10⁻⁶)/(8.85 × 10⁻¹²)
- Calculate: E = 3.39 × 10⁵ N/C
Answer: The electric field just outside the plate is 3.39 × 10⁵ N/C, directed away from the plate (since the charge is positive).
Conductors in External Electric Fields
Induction Process
When a conductor is placed in an external electric field:
- Initial state: External field penetrates the conductor
- Electron movement: Free electrons move in response to the field
- Charge separation: Positive and negative charges separate
- Induced field: Induced charges create their own electric field
- Equilibrium: Induced field cancels external field inside conductor
Faraday Cage Effect
A hollow conductor completely shields its interior from external electric fields:
- Complete shielding: No electric field inside the cavity
- Charge distribution: All excess charge resides on outer surface
- Applications: Electronic shielding, microwave ovens, MRI rooms
Applications of Conductors
- Electrostatic shielding: Protecting sensitive electronics from electric fields
- Lightning rods: Using sharp points to concentrate electric field
- Capacitors: Using conductors as plates to store charge
- Electrical wiring: Conducting electric current through circuits
- Grounding: Providing a path for excess charge to flow to earth
Common Mistakes to Avoid
⚠️ Common Errors
- Thinking field exists inside: Electric field inside conductor is always zero in equilibrium
- Ignoring surface charge: All excess charge must be on the surface
- Forgetting perpendicular field: Field at surface is always perpendicular
- Confusing with insulators: Conductors and insulators behave very differently
Practice Problems
Practice Problem 1
Problem: A conducting sphere of radius 4.0 cm has a surface charge density of +2.0 × 10⁻⁶ C/m². What is the electric field just outside the sphere?
Click for solution
Solution:
- Given: σ = +2.0 × 10⁻⁶ C/m², ε₀ = 8.85 × 10⁻¹² C²/N⋅m²
- Formula: E = σ/ε₀
- Substitute: E = (2.0 × 10⁻⁶)/(8.85 × 10⁻¹²)
- Calculate: E = 2.26 × 10⁵ N/C
Answer: 2.26 × 10⁵ N/C, directed away from the sphere
Practice Problem 2
Problem: A conducting cube has a total charge of +6.0 μC. If the cube has side length 2.0 cm, what is the surface charge density?
Click for solution
Solution:
- Given: Q = +6.0 × 10⁻⁶ C, side length = 2.0 × 10⁻² m
- Surface area: A = 6 × (2.0 × 10⁻²)² = 2.4 × 10⁻³ m²
- Surface charge density: σ = Q/A = (6.0 × 10⁻⁶)/(2.4 × 10⁻³)
- Calculate: σ = 2.5 × 10⁻³ C/m²
Answer: 2.5 × 10⁻³ C/m²
Charge Sharing Between Conducting Spheres of Different Sizes
Key Principle
When two conducting spheres of different radii are brought into contact and then separated, the final charge on each sphere is not simply the average of their initial charges. Instead, charge distributes so that both spheres reach the same electric potential (voltage), because conductors in equilibrium are equipotentials.
For isolated spheres of radii R₁ and R₂ with initial charges q₁ and q₂:
Potential of a sphere: \( V = \frac{1}{4\pi\epsilon_0} \frac{q}{R} \)
After contact and separation, set \( V_1 = V_2 \):
\( \frac{q_1'}{R_1} = \frac{q_2'}{R_2} \)
and \( q_1' + q_2' = q_1 + q_2 \) (conservation of charge)
Solving gives:
\( q_1' = (q_1 + q_2) \frac{R_1}{R_1 + R_2} \)
\( q_2' = (q_1 + q_2) \frac{R_2}{R_1 + R_2} \)
Example: Charge Sharing for Different Sized Spheres
Problem: Sphere A (radius 2 cm) has +6 μC, Sphere B (radius 6 cm) has -2 μC. They are brought into contact and then separated. What is the final charge on each?
Solution Steps:
- Total charge: \( q_{\text{total}} = +6 \text{ μC} + (-2 \text{ μC}) = +4 \text{ μC} \)
- Radii: \( R_1 = 2 \text{ cm}, R_2 = 6 \text{ cm} \)
- Formula: \( q_1' = q_{\text{total}} \frac{R_1}{R_1 + R_2} \), \( q_2' = q_{\text{total}} \frac{R_2}{R_1 + R_2} \)
- Calculate: \( q_1' = 4 \times \frac{2}{2+6} = 1 \text{ μC} \), \( q_2' = 4 \times \frac{6}{2+6} = 3 \text{ μC} \)
Answer: After contact, Sphere A has +1 μC, Sphere B has +3 μC.
Key Concepts Summary
- Electric field inside conductor is zero in electrostatic equilibrium
- Excess charge resides on the surface of conductors
- Surface charge density determines electric field at surface
- Conductors shield their interior from external electric fields
- Charge distribution depends on surface curvature
- Conductors form equipotential surfaces in electrostatic equilibrium
Quick Reference
- Field inside conductor: \(E_{\text{inside}} = 0\)
- Field at surface: \(E = \frac{\sigma}{\epsilon_0}\)
- Surface charge density: \(\sigma = \frac{Q}{A}\)
- Conductor properties: Free electrons, equipotential surface, surface charge
- Shielding: Complete protection from external fields