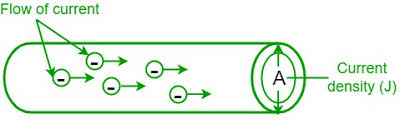
Current Density
Current density is a vector quantity that describes the current per unit area flowing through a conductor. It provides a more detailed description of how current is distributed within a material and is essential for understanding current flow in conductors of varying cross-sectional areas.
Definition of Current Density
Current density is defined as the current per unit area, where the direction is specified by the unit vector \(\hat{n}\) in the direction of current flow.
- Units: A/m² (amperes per square meter)
- Direction: Same as conventional current direction
- Vector quantity: Has both magnitude and direction
- Microscopic description: Provides detailed current distribution
Relationship to Current
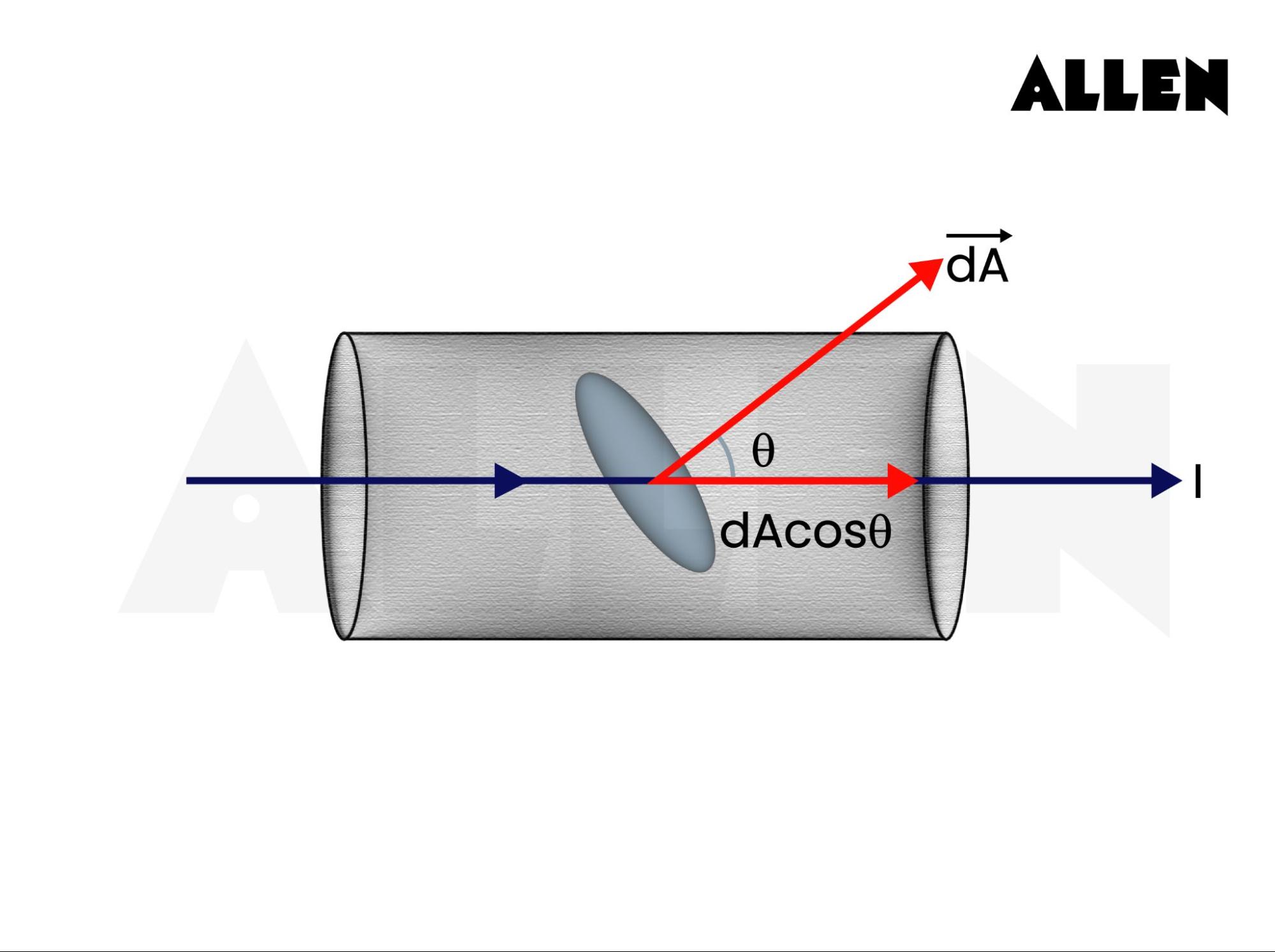
The total current through a surface is the flux of current density through that surface. For uniform current density, this simplifies to:
- Where:
- \(I\) = total current
- \(J\) = current density magnitude
- \(A\) = cross-sectional area
- \(\theta\) = angle between current density and area normal
- Perpendicular flow: When \(\theta = 0°\), \(I = JA\)
- Parallel flow: When \(\theta = 90°\), \(I = 0\)
Microscopic Expression
Current density can also be expressed in terms of the microscopic properties of the conductor.
- Where:
- \(n\) = number density of charge carriers
- \(q\) = charge of each carrier
- \(\vec{v}_d\) = drift velocity vector
- For electrons: \(q = -e\) (negative charge)
- For holes: \(q = +e\) (positive charge)
- Direction: Opposite to electron drift velocity
Memory Trick: NEVADA for Current Density
Remember the current density formula using NEVADA:
- NE = \(ne\) (number density × elementary charge)
- V = drift velocity (\(v_d\))
- A = area (related to current density)
- D = density (current density \(J\))
- A = area again (cross-sectional area)
So: \(ne \times v_d = J\) (current density)
And: \(J \times A = I\) (total current)
This helps you remember that \(nev_d = J\), which is the microscopic expression for current density!
Current Density in Different Geometries
Uniform Current Density
When current density is constant across the cross-section:
Non-Uniform Current Density
When current density varies across the cross-section, the total current is:
Example: Radial Current Density
Problem: A cylindrical conductor has current density that varies with radius as \(J(r) = J_0(1 - r/R)\), where \(R\) is the radius. Find the total current.
Solution:
- Area element: \(dA = 2\pi r \, dr\)
- Current element: \(dI = J(r) \, dA = J_0(1 - r/R) \cdot 2\pi r \, dr\)
- Total current: \(I = \int_0^R J_0(1 - r/R) \cdot 2\pi r \, dr\)
- Integration: \(I = 2\pi J_0 \int_0^R (r - r^2/R) \, dr\)
- Result: \(I = 2\pi J_0 [R^2/2 - R^2/3] = \pi J_0 R^2/3\)
Answer: The total current is \(\frac{\pi J_0 R^2}{3}\).
Current Density and Ohm's Law
At the microscopic level, the electric field in a conductor is proportional to the current density, with resistivity as the proportionality constant.
- Where:
- \(\vec{E}\) = electric field
- \(\rho\) = resistivity
- \(\vec{J}\) = current density
- Conductivity: \(\sigma = \frac{1}{\rho}\)
- Alternative form: \(\vec{J} = \sigma\vec{E}\)
Worked Examples
Example 1: Basic Current Density Calculation
Problem: A wire with radius 1.0 mm carries a current of 2.0 A. What is the current density in the wire?
Solution:
- Cross-sectional area: \(A = \pi r^2 = \pi(1.0 \times 10^{-3} \text{ m})^2 = 3.14 \times 10^{-6} \text{ m}^2\)
- Current density: \(J = \frac{I}{A} = \frac{2.0 \text{ A}}{3.14 \times 10^{-6} \text{ m}^2}\)
- Calculation: \(J = 6.37 \times 10^5 \text{ A/m}^2\)
Answer: The current density is 6.37 × 10⁵ A/m².
Example 2: Current Density from Microscopic Properties
Problem: A copper wire has 8.5 × 10²⁸ free electrons per m³. If the drift velocity is 1.0 × 10⁻⁴ m/s, what is the current density?
Solution:
- Current density formula: \(J = nqv_d\)
- For electrons: \(q = -e = -1.602 \times 10^{-19} \text{ C}\)
- Substitution: \(J = (8.5 \times 10^{28} \text{ m}^{-3})(1.602 \times 10^{-19} \text{ C})(1.0 \times 10^{-4} \text{ m/s})\)
- Calculation: \(J = 1.36 \times 10^6 \text{ A/m}^2\)
Answer: The current density is 1.36 × 10⁶ A/m².
Example 3: Current from Non-Uniform Current Density
Problem: A wire has current density that varies as \(J(r) = J_0 r/R\), where \(R\) is the radius. If \(J_0 = 2.0 \times 10^6 \text{ A/m}^2\) and \(R = 1.0 \text{ mm}\), find the total current.
Solution:
- Current element: \(dI = J(r) \cdot 2\pi r \, dr = J_0 \frac{r}{R} \cdot 2\pi r \, dr\)
- Total current: \(I = 2\pi J_0 \int_0^R \frac{r^2}{R} \, dr\)
- Integration: \(I = 2\pi J_0 \frac{R^2}{3}\)
- Substitution: \(I = 2\pi(2.0 \times 10^6) \frac{(1.0 \times 10^{-3})^2}{3}\)
- Result: \(I = 4.19 \text{ A}\)
Answer: The total current is 4.19 A.
Example 4: Electric Field from Current Density
Problem: A copper wire has current density 1.0 × 10⁶ A/m². If copper has resistivity 1.68 × 10⁻⁸ Ω·m, what is the electric field in the wire?
Solution:
- Microscopic Ohm's law: \(E = \rho J\)
- Substitution: \(E = (1.68 \times 10^{-8} \text{ Ω·m})(1.0 \times 10^6 \text{ A/m}^2)\)
- Calculation: \(E = 1.68 \times 10^{-2} \text{ V/m}\)
Answer: The electric field is 1.68 × 10⁻² V/m.
Example 5: Current Density in Parallel Wires
Problem: Two wires are connected in parallel. Wire A has radius 1.0 mm and carries 3.0 A. Wire B has radius 2.0 mm and carries 5.0 A. Which wire has higher current density?
Solution:
- Wire A area: \(A_A = \pi(1.0 \times 10^{-3})^2 = 3.14 \times 10^{-6} \text{ m}^2\)
- Wire A current density: \(J_A = \frac{3.0}{3.14 \times 10^{-6}} = 9.55 \times 10^5 \text{ A/m}^2\)
- Wire B area: \(A_B = \pi(2.0 \times 10^{-3})^2 = 1.26 \times 10^{-5} \text{ m}^2\)
- Wire B current density: \(J_B = \frac{5.0}{1.26 \times 10^{-5}} = 3.98 \times 10^5 \text{ A/m}^2\)
Answer: Wire A has higher current density (9.55 × 10⁵ A/m² vs 3.98 × 10⁵ A/m²).
Current Density Visualization
Explore how current density varies with different wire geometries: