Dielectric Basics
A dielectric is an insulating material that, when placed between the plates of a capacitor, increases its capacitance. Understanding dielectrics is essential for designing capacitors and understanding how they work in various applications.
What is a Dielectric?
A dielectric is a non-conducting material (insulator) that can be polarized by an electric field. When placed between capacitor plates, it increases the capacitance by reducing the electric field strength and allowing more charge to be stored.
Key Properties of Dielectrics
- Insulating: Do not conduct electric current
- Polarizable: Can be polarized by an electric field
- Dielectric constant: Measure of how much the material increases capacitance
Dielectric Constant (κ)
Dielectric Constant Formula
$$\kappa = \frac{C}{C_0}$$
Where:
- κ = Dielectric constant (dimensionless)
- C = Capacitance with dielectric
- C₀ = Capacitance without dielectric (vacuum)
The dielectric constant (also called relative permittivity) is always greater than 1 for real materials. It tells us how much the capacitance increases when a dielectric is inserted.
Common Dielectric Constants
| Material | Dielectric Constant (κ) | Common Uses |
|---|---|---|
| Vacuum | 1.0 | Reference standard |
| Air | 1.0006 | Air capacitors |
| Paper | 2.0-3.5 | Paper capacitors |
| Mica | 3.0-7.0 | High-voltage capacitors |
| Glass | 4.0-10.0 | High-voltage applications |
| Porcelain | 5.0-7.0 | Power capacitors |
| Aluminum Oxide | 8.0-10.0 | Electrolytic capacitors |
| Ceramic (low-k) | 6.0-15.0 | General purpose |
| Ceramic (high-k) | 100-10,000 | Miniature capacitors |
| Water | 80.4 | Not used in capacitors |
How Dielectrics Work
Polarization Process
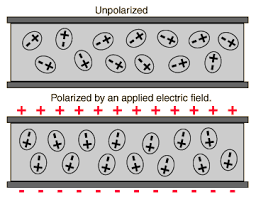
When a dielectric is placed in an electric field, several things happen:
Polarization Steps:
- Electric field applied: External field creates force on charges
- Charge separation: Positive and negative charges separate slightly
- Dipole formation: Creates many small electric dipoles
- Internal field: Dipoles create internal field opposite to external field
- Net field reduction: Total field inside dielectric is reduced
Effect on Capacitance
The presence of a dielectric increases capacitance in two ways:
- Reduced electric field: The dielectric reduces the electric field strength
- Increased charge storage: More charge can be stored for the same voltage
Capacitance with Dielectric
$$C = \kappa C_0$$
Where:
- C = Capacitance with dielectric
- κ = Dielectric constant
- C₀ = Capacitance without dielectric
Types of Dielectric Polarization
Electronic Polarization
Mechanism: Electron clouds shift relative to nuclei
Speed: Very fast (10⁻¹⁵ seconds)
Materials: All materials
Frequency response: Works at all frequencies
Ionic Polarization
Mechanism: Positive and negative ions move in opposite directions
Speed: Fast (10⁻¹³ seconds)
Materials: Ionic crystals (NaCl, etc.)
Frequency response: Works up to infrared frequencies
Oriental Polarization
Mechanism: Permanent dipoles align with electric field
Speed: Slower (10⁻¹⁰ seconds)
Materials: Polar molecules (water, etc.)
Frequency response: Works up to microwave frequencies
Worked Examples
Example 1: Capacitance with Dielectric
Problem: A parallel plate capacitor has a capacitance of 10 pF in air. If a dielectric with κ = 4.0 is inserted, what is the new capacitance?
Solution Steps:
- Given: C₀ = 10 pF, κ = 4.0
- Formula: C = κC₀
- Substitute: C = 4.0 × 10 pF
- Calculate: C = 40 pF
Answer: The capacitance increases to 40 pF.
Example 2: Finding Dielectric Constant
Problem: A capacitor has a capacitance of 5 μF in vacuum and 25 μF with a dielectric. What is the dielectric constant?
Solution Steps:
- Given: C₀ = 5 μF, C = 25 μF
- Formula: κ = C/C₀
- Substitute: κ = 25/5
- Calculate: κ = 5.0
Answer: The dielectric constant is 5.0.
Example 3: Energy Storage with Dielectric
Problem: A 2 μF capacitor is charged to 12 V in air, then a dielectric with κ = 3.0 is inserted while maintaining the charge. What is the new voltage and energy?
Solution Steps:
- Step 1 - Original charge: Q = CV = 2 × 12 = 24 μC
- Step 2 - New capacitance: C_new = κC = 3 × 2 = 6 μF
- Step 3 - New voltage: V_new = Q/C_new = 24/6 = 4 V
- Step 4 - New energy: E = ½CV² = ½ × 6 × 4² = 48 μJ
Answer: The voltage drops to 4 V and the energy decreases to 48 μJ.
Interactive Dielectric Calculator
Calculate Capacitance with Dielectric
Capacitor Parameters
Results
Applications of Dielectrics
Capacitor Design
- High capacitance: High-κ materials for miniature capacitors
- Temperature stability: Materials with stable κ over temperature
- Frequency response: Materials suitable for specific frequency ranges
Electronic Applications
- Insulation: Preventing electrical breakdown
- Energy storage: Increasing energy density in capacitors
- Signal processing: Filtering and coupling circuits
- Memory devices: Ferroelectric materials for non-volatile memory
Industrial Applications
- Power transmission: High-voltage cable insulation
- Electronics packaging: Printed circuit board materials
- Medical devices: Biocompatible dielectric materials
- Automotive: Ignition systems and sensors
Common Mistakes to Avoid
⚠️ Common Errors
- Wrong formula: Using C = κ/C₀ instead of C = κC₀
- Unit confusion: Forgetting that κ is dimensionless
- Frequency effects: Ignoring dielectric losses at high frequencies
- Temperature effects: Not accounting for κ changes with temperature
Practice Problems
Practice Problem 1
Problem: A capacitor has a capacitance of 8 pF in air. If a dielectric with κ = 6.0 is inserted, what is the new capacitance?
Click for solution
Solution:
- Given: C₀ = 8 pF, κ = 6.0
- Formula: C = κC₀
- Substitute: C = 6.0 × 8 pF
- Calculate: C = 48 pF
Answer: 48 pF
Practice Problem 2
Problem: A 3 μF capacitor is charged to 15 V, then a dielectric with κ = 2.5 is inserted while maintaining the charge. What is the new voltage?
Click for solution
Solution:
- Step 1 - Original charge: Q = CV = 3 × 15 = 45 μC
- Step 2 - New capacitance: C_new = κC = 2.5 × 3 = 7.5 μF
- Step 3 - New voltage: V_new = Q/C_new = 45/7.5 = 6 V
Answer: 6 V
Key Concepts Summary
- Dielectric constant: κ = C/C₀, always > 1 for real materials
- Capacitance increase: C = κC₀ when dielectric is inserted
- Polarization: Dielectrics reduce electric field by creating internal dipoles
- Energy storage: Dielectrics can increase or decrease energy depending on conditions
- Applications: Used in capacitors, insulation, and electronic devices
Quick Reference
- Dielectric constant: κ = C/C₀
- Capacitance with dielectric: C = κC₀
- Electric field reduction: E = E₀/κ
- Energy with constant charge: E = E₀/κ
- Energy with constant voltage: E = κE₀