← Back to Concepts

Electric Charge and Conservation

Electric charge is one of the most fundamental properties of matter. It is the source of all electrical phenomena and forms the foundation of electromagnetism. Understanding electric charge and its conservation is essential for analyzing electric forces, fields, and circuits.

What is Electric Charge?

$$q = \text{fundamental property of matter}$$

Electric charge is a fundamental property of matter that determines how objects interact electrically. There are two types of charge: positive and negative. Like charges repel each other, while opposite charges attract.

Positive and negative charges with their interactions.

Positive charge is typically associated with protons.
Negative charge is typically associated with electrons.
Charge is a scalar quantity with magnitude but no direction.
The smallest unit of charge is the elementary charge (the charge of a proton) $e = 1.602 \times 10^{-19}$ C.
The charge of an electron is $-e$.

Key Properties of Electric Charge

Units: Coulombs (C)
Charge is always conserved in isolated systems.
Charge is quantized - it comes in discrete units of $e$. 1e, 2e, 3e, etc. You can't have 1.5e or 0.7e.
Charge is invariant - it doesn't change with velocity or reference frame.

Finding Total Charge from Charge Density

$$Q = \int \rho(\vec{r})\, dV$$

When charge is distributed continuously (not just as point charges), we use charge density to describe how much charge is present per unit length, area, or volume:

Linear charge density: $\lambda = \frac{dq}{dl}$ (C/m)
Surface charge density: $\sigma = \frac{dq}{dA}$ (C/m²)
Volume charge density: $\rho = \frac{dq}{dV}$ (C/m³)

To find the total charge in a region, integrate the charge density over the appropriate dimension:

Line: $Q = \int \lambda(x)\, dx$
Surface: $Q = \int \sigma(x, y)\, dA$
Volume: $Q = \int \rho(x, y, z)\, dV$

Example: Total Charge on a Non-Uniform Rod

Problem: A thin rod of length 2 m has a linear charge density $\lambda(x) = 3x$ C/m, where $x$ is in meters from one end. What is the total charge on the rod?

Solution:

Set up the integral: $Q = \int_0^2 3x\, dx$
Integrate: $Q = 3 \int_0^2 x\, dx = 3 \left[\frac{1}{2}x^2\right]_0^2 = 3 \times \frac{1}{2} \times 4 = 6$ C

Answer: The total charge on the rod is 6 C.

Example: Total Charge on a Disk (Surface Charge Density)

Problem: A circular disk of radius 0.5 m has a uniform surface charge density $\sigma = 2$ C/m². What is the total charge on the disk?

Solution:

Area of the disk: $A = \pi r^2 = \pi (0.5)^2 = 0.25\pi$ m²
Total charge: $Q = \sigma A = 2 \times 0.25\pi = 0.5\pi$ C
Numerical value: $Q \approx 1.57$ C

Answer: The total charge on the disk is approximately 1.57 C.

Example: Total Charge in a Sphere (Volume Charge Density)

Problem: A solid sphere of radius 0.2 m has a uniform volume charge density $\rho = 5$ C/m³. What is the total charge in the sphere?

Solution:

Volume of the sphere: $V = \frac{4}{3}\pi r^3 = \frac{4}{3}\pi (0.2)^3 = \frac{4}{3}\pi (0.008) = 0.0107\pi$ m³
Total charge: $Q = \rho V = 5 \times 0.0107\pi = 0.0535\pi$ C
Numerical value: $Q \approx 0.168$ C

Answer: The total charge in the sphere is approximately 0.168 C.

Conservation of Charge

$$\sum q_{\text{initial}} = \sum q_{\text{final}}$$

The total electric charge in an isolated system remains constant. This is one of the most fundamental conservation laws in physics. Charge can be transferred between objects, but it cannot be created or destroyed.

Conservation of Charge — Total charge remains constant in isolated systems.

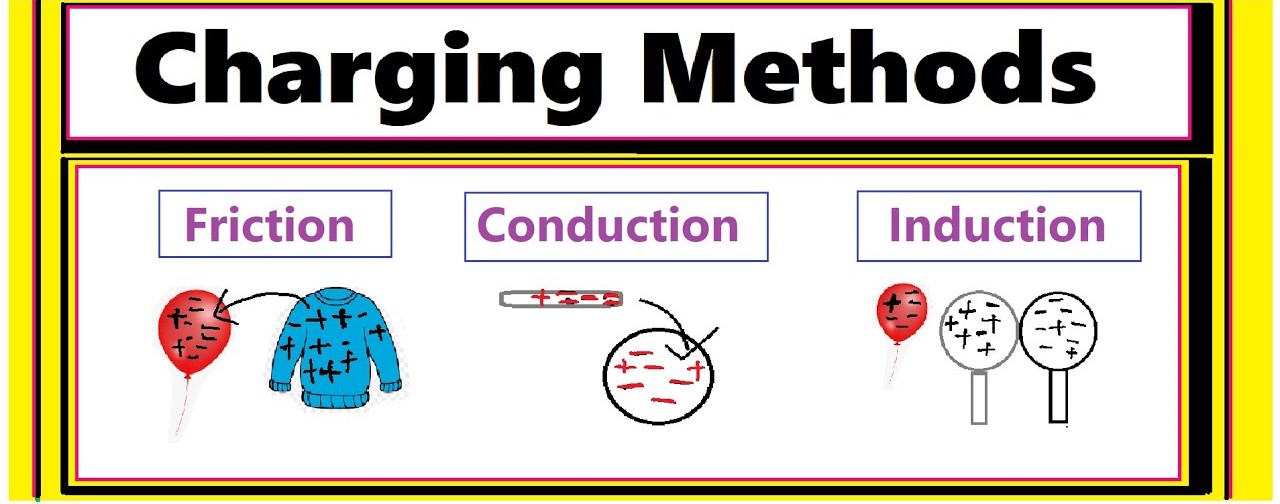
Charge Transfer Mechanisms

$$\text{Conduction: } q_{\text{final}} = \frac{q_1 + q_2}{2}$$

There are three main ways charge can be transferred:

Conduction: Direct contact between objects allows electrons to flow.
Induction: Bringing a charged object near a neutral object causes charge separation.
Friction: Rubbing two objects together can transfer electrons between them.

Understanding these mechanisms is crucial for analyzing how objects become charged and how charge distributions affect electric fields and forces.

Charge Transfer Mechanisms — Visual representation of conduction, induction, and friction.

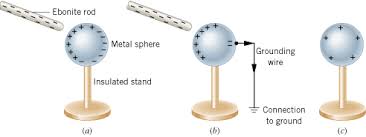
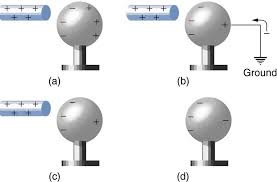
Grounding and Charge Neutralization

$$\text{When grounded: } q_{\text{final}} = 0$$

Grounding is the process of connecting a charged object to the Earth (or a large conductor) to neutralize its charge. The Earth acts as an infinite reservoir of charge, allowing excess electrons to flow away or providing electrons to neutralize positive charges.

Positive charge: Electrons flow from Earth to neutralize the positive charge.
Negative charge: Excess electrons flow to Earth, leaving the object neutral.
Neutralization: The object becomes electrically neutral (net charge = 0).

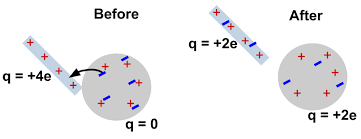
Worked Examples

Example 1: Charge Conservation in Conduction

Problem: Two identical metal spheres have charges of +8 μC and -4 μC respectively. If they are brought into contact and then separated, what will be the final charge on each sphere?

Solution:

Initial total charge: $q_{\text{total}} = +8 \text{ μC} + (-4 \text{ μC}) = +4 \text{ μC}$
Conservation principle: Total charge remains +4 μC after contact
Equal distribution: Since spheres are identical, charge distributes equally
Final charge per sphere: $q_{\text{final}} = \frac{+4 \text{ μC}}{2} = +2 \text{ μC}$

Answer: Each sphere will have a charge of +2 μC.

Example 2: Charge Transfer by Induction

Problem: A neutral conducting sphere is brought near a positively charged rod. The sphere is then grounded while the rod is still nearby. What happens to the sphere's charge when the ground connection is removed and then the rod is taken away?

Solution:

Initial state: Sphere is neutral (net charge = 0)
Induction: Positive rod attracts electrons to near side, repels protons to far side
Grounding: Excess electrons flow to ground, leaving sphere with net positive charge
Rod removal: Electrons redistribute, but sphere retains net positive charge

Answer: The sphere ends up with a net positive charge.

Example 3: Quantized Charge Calculation

Problem: An object has a charge of -3.2 × 10⁻¹⁹ C. How many excess electrons does it have?

Solution:

Elementary charge: $e = 1.602 \times 10^{-19} \text{ C}$
Number of electrons: $n = \frac{|q|}{e} = \frac{3.2 \times 10^{-19} \text{ C}}{1.602 \times 10^{-19} \text{ C}}$
Calculation: $n = \frac{3.2}{1.602} = 2$

Answer: The object has 2 excess electrons.

Example 4: Complex Charge Distribution

Problem: Three identical conducting spheres A, B, and C have initial charges of +6 μC, -2 μC, and +4 μC respectively. Sphere A touches sphere B, then sphere A touches sphere C. What are the final charges on each sphere?

Solution:

First contact (A and B):
- Total charge: $q_{\text{total}} = +6 \text{ μC} + (-2 \text{ μC}) = +4 \text{ μC}$
- After contact: $q_A = q_B = \frac{+4 \text{ μC}}{2} = +2 \text{ μC}$
Second contact (A and C):
- Total charge: $q_{\text{total}} = +2 \text{ μC} + (+4 \text{ μC}) = +6 \text{ μC}$
- After contact: $q_A = q_C = \frac{+6 \text{ μC}}{2} = +3 \text{ μC}$

Answer: Final charges are: A = +3 μC, B = +2 μC, C = +3 μC

Example 5: Charge Neutralization

Problem: A plastic rod rubbed with wool acquires a charge of -8 × 10⁻⁹ C. How many electrons were transferred during the rubbing process?

Solution:

Given: $q = -8 \times 10^{-9} \text{ C}$ (negative indicates excess electrons)
Elementary charge: $e = 1.602 \times 10^{-19} \text{ C}$
Number of electrons: $n = \frac{|q|}{e} = \frac{8 \times 10^{-9} \text{ C}}{1.602 \times 10^{-19} \text{ C}}$
Calculation: $n = \frac{8 \times 10^{-9}}{1.602 \times 10^{-19}} = 5 \times 10^{10}$

Answer: Approximately 5 × 10¹⁰ electrons were transferred to the rod.

Induction Animation

Watch how a charged rod induces charge separation in a neutral ball, and how grounding affects the process: