Electric Field Definition
The electric field is a fundamental concept in electromagnetism that describes how electric charges influence the space around them. Understanding electric fields is crucial for analyzing electric forces, potential energy, and electromagnetic phenomena.
What is an Electric Field?
The electric field at a point in space is defined as the electric force per unit charge that would be experienced by a small positive test charge placed at that point. The direction of the field is the direction of the force on a positive test charge.
- E: Electric field vector (N/C or V/m)
- F: Electric force on test charge (N)
- q₀: Test charge (C)
Relating Electric Fields to Gravitational Fields
Gravitational Field Analogy
Just as Earth creates a gravitational field that affects all objects with mass, electric charges create electric fields that affect all objects with charge.

Key Similarities
- Field concept: Both describe how a source affects surrounding space
- Force per unit: Gravitational field = F/m, Electric field = F/q
- Inverse square law: Both fields decrease with distance squared
- Superposition: Multiple sources add their fields together
Key Differences
- Charge types: Electric fields can be positive or negative, gravitational fields are always attractive
- Strength: Electric forces are much stronger than gravitational forces
- Shielding: Electric fields can be shielded, gravitational fields cannot
Electric Field Due to a Point Charge
For a point charge q, the electric field at distance r is given by Coulomb's Law divided by the test charge. The field points away from positive charges and toward negative charges.
- E: Electric field magnitude (N/C)
- k: Coulomb's constant = 8.99 × 10⁹ N⋅m²/C²
- q: Source charge (C)
- r: Distance from charge (m)
- r̂: Unit vector pointing from charge to field point
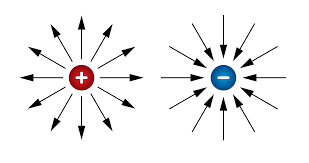
Electric Field Lines
Electric field lines are a visual representation of electric fields that show:
- Direction: Field lines point in the direction of the electric field
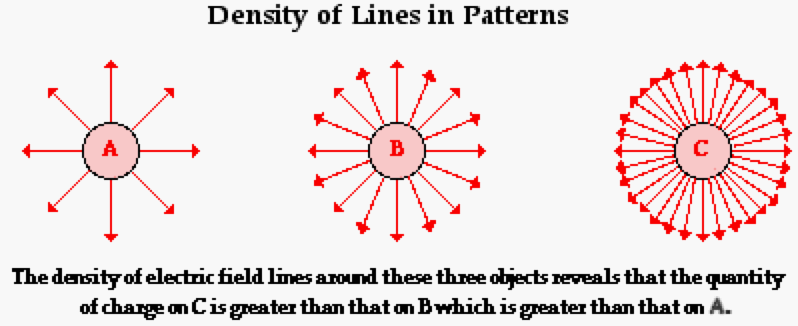
- Strength: Closer lines indicate stronger fields
- Rules: Lines never cross and always start on positive charges, end on negative charges
- Density: More lines per area means stronger field
Superposition Principle
The total electric field due to multiple charges is the vector sum of the individual electric fields. This principle allows us to calculate complex field patterns by adding simpler contributions.
Worked Examples
Example 1: Electric Field from a Point Charge
Problem: Calculate the electric field 2.0 m from a point charge of +3.0 μC.
Solution:
- Given: q = +3.0 × 10⁻⁶ C, r = 2.0 m
- Formula: \(E = k\frac{q}{r^2}\)
- Calculation: \(E = (8.99 \times 10^9) \frac{3.0 \times 10^{-6}}{(2.0)^2}\)
- Result: \(E = 6.74 \times 10^3 \text{ N/C}\)
Answer: The electric field is 6.74 × 10³ N/C, pointing away from the positive charge.
Example 2: Electric Field Between Two Charges
Problem: Two point charges, +2.0 μC and -1.0 μC, are placed 3.0 m apart. Find the electric field at the midpoint between them.
Solution:
- Field from +2.0 μC: \(E_1 = k\frac{2.0 \times 10^{-6}}{(1.5)^2} = 8.0 \times 10^3 \text{ N/C}\) (away)
- Field from -1.0 μC: \(E_2 = k\frac{1.0 \times 10^{-6}}{(1.5)^2} = 4.0 \times 10^3 \text{ N/C}\) (toward)
- Both fields point right: \(E_{\text{total}} = 8.0 \times 10^3 + 4.0 \times 10^3 = 12.0 \times 10^3 \text{ N/C}\)
Answer: The electric field at the midpoint is 12.0 × 10³ N/C, pointing toward the negative charge.
Electric Field vs. Gravitational Field Comparison
| Property | Gravitational Field | Electric Field |
|---|---|---|
| Definition | g = F/m | E = F/q |
| Units | N/kg | N/C |
| Direction | Always attractive | Repulsive or attractive |
| Source | Mass | Charge |
| Strength | Weak | Strong |