Electric Potential Energy
Electric potential energy is the energy stored in a system of charges due to their positions relative to each other. It represents the work done to assemble the charge configuration and is a fundamental concept in electrostatics.
What is Electric Potential Energy?
The value "zero" for electric potential energy (EPE) is always relative—it depends on where you choose your reference point and the sign of the charges involved. For two charges, we usually define EPE = 0 when they are infinitely far apart. But:
- For like charges (both positive or both negative), EPE is positive when they are close, and zero means they are infinitely far apart (no interaction).
- For unlike charges (one positive, one negative), EPE is negative when they are close, and zero still means infinitely far apart—but in this case, "zero" can mean the system has released a lot of energy as the charges came together.
Electric potential energy is the work required to bring charges from infinity to their current positions. It depends on the charges involved and their separation distance.
- U: Electric potential energy (J)
- k: Coulomb's constant = 8.99 × 10⁹ N⋅m²/C²
- q₁, q₂: Charges (C)
- r: Distance between charges (m)
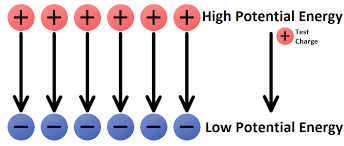 Work is done to bring charges together, storing potential energy.
Work is done to bring charges together, storing potential energy.
Relationship to Work
Work-Energy Principle
The electric potential energy equals the work done by an external force to assemble the charge configuration:
$$W = \Delta U = U_f - U_i$$
When charges are moved by an external force:
- Positive work: External force does work on the system (energy increases)
- Negative work: Electric force does work (energy decreases)
- Zero work: Charges move perpendicular to field lines
Sign of Electric Potential Energy
Energy Sign Rules
- Positive energy: Like charges (repulsion) - work needed to bring them together
- Negative energy: Unlike charges (attraction) - work is released when they come together
- Zero energy: At infinite separation
Multiple Charge Systems
For multiple charges, the total potential energy is the sum of all pairwise interactions. Each pair contributes a term to the total energy.
Example: Three Charges
For three charges q₁, q₂, q₃:
$$U = k\left(\frac{q_1 q_2}{r_{12}} + \frac{q_1 q_3}{r_{13}} + \frac{q_2 q_3}{r_{23}}\right)$$
Worked Examples
Example 1: Two Point Charges
Problem: Calculate the electric potential energy of two charges: +3.0 μC and -2.0 μC, separated by 2.0 m.
Solution Steps:
- Given: q₁ = +3.0 × 10⁻⁶ C, q₂ = -2.0 × 10⁻⁶ C, r = 2.0 m
- Formula: \(U = k\frac{q_1 q_2}{r}\)
- Substitute: \(U = (8.99 \times 10^9) \frac{(+3.0 \times 10^{-6})(-2.0 \times 10^{-6})}{2.0}\)
- Calculate: \(U = (8.99 \times 10^9) \frac{-6.0 \times 10^{-12}}{2.0}\)
- Result: \(U = -2.7 \times 10^{-2} \text{ J}\)
Answer: The electric potential energy is -2.7 × 10⁻² J (negative because unlike charges attract).
Example 2: Work Required to Separate Charges
Problem: Two charges of +1.0 μC each are initially 1.0 m apart. How much work is required to separate them to 3.0 m?
Solution Steps:
- Initial energy: \(U_i = k\frac{(1.0 \times 10^{-6})^2}{1.0} = 9.0 \times 10^{-3} \text{ J}\)
- Final energy: \(U_f = k\frac{(1.0 \times 10^{-6})^2}{3.0} = 3.0 \times 10^{-3} \text{ J}\)
- Work required: \(W = U_f - U_i = 3.0 \times 10^{-3} - 9.0 \times 10^{-3}\)
- Result: \(W = -6.0 \times 10^{-3} \text{ J}\)
Answer: -6.0 × 10⁻³ J (negative work means the electric force does the work).
Example 3: Three Charge System
Problem: Three charges are placed at the corners of an equilateral triangle: +2.0 μC at each corner. The side length is 1.0 m. Find the total electric potential energy.
Solution Steps:
- Each pair interaction: \(U_{pair} = k\frac{(2.0 \times 10^{-6})^2}{1.0} = 3.6 \times 10^{-2} \text{ J}\)
- Three pairs: Total energy = 3 × U_pair
- Calculate: \(U_{total} = 3 \times 3.6 \times 10^{-2} = 1.08 \times 10^{-1} \text{ J}\)
Answer: The total electric potential energy is 1.08 × 10⁻¹ J.
Electric Potential Energy vs. Electric Potential
| Property | Electric Potential Energy (U) | Electric Potential (V) |
|---|---|---|
| Definition | Energy of charge system | Energy per unit charge |
| Units | Joules (J) | Volts (V = J/C) |
| Formula | U = kq₁q₂/r | V = kq/r |
| Dependence | Depends on all charges | Depends on source charge only |
| Use | System energy analysis | Field strength analysis |
Applications of Electric Potential Energy
- Capacitors: Energy stored in electric fields between plates
- Batteries: Chemical energy converted to electrical potential energy
- Particle accelerators: Work done to separate charges
- Lightning: Release of stored electric potential energy
- Electron orbits: Energy levels in atoms
Conservation of Energy
Energy Conservation Principle
In an isolated system, the total energy (kinetic + potential) remains constant:
$$K_i + U_i = K_f + U_f$$
This principle allows us to:
- Calculate speeds: Convert potential energy to kinetic energy
- Find escape velocities: Minimum speed to overcome attraction
- Analyze orbits: Balance of kinetic and potential energy
- Predict motion: How charges will move in electric fields
Practice Problems
Practice Problem 1
Problem: A charge of +5.0 μC is moved from infinity to a point 2.0 m from a fixed charge of +3.0 μC. How much work is done?
Click for solution
Solution:
- Initial energy: U_i = 0 (at infinity)
- Final energy: \(U_f = k\frac{(5.0 \times 10^{-6})(3.0 \times 10^{-6})}{2.0}\)
- Work done: \(W = U_f - U_i = 6.7 \times 10^{-2} \text{ J}\)
Answer: 6.7 × 10⁻² J
Practice Problem 2
Problem: Two electrons are initially 1.0 nm apart. What is their electric potential energy?
Click for solution
Solution:
- Electron charge: q = -1.6 × 10⁻¹⁹ C
- Distance: r = 1.0 × 10⁻⁹ m
- Energy: \(U = k\frac{(-1.6 \times 10^{-19})^2}{1.0 \times 10^{-9}}\)
- Result: \(U = 2.3 \times 10^{-19} \text{ J}\)
Answer: 2.3 × 10⁻¹⁹ J
Key Concepts Summary
- Electric potential energy is the work required to assemble a charge configuration
- Positive energy means like charges (repulsion)
- Negative energy means unlike charges (attraction)
- Energy is conserved in isolated systems
- Work equals energy change when charges are moved
Quick Reference
- Two charges: \(U = k\frac{q_1 q_2}{r}\)
- Multiple charges: \(U = k\sum_{i < j} \frac{q_i q_j}{r_{ij}}\)
- Work: \(W = \Delta U = U_f - U_i\)
- Conservation: \(K_i + U_i = K_f + U_f\)