Electric Potential
Electric potential is a scalar quantity that represents the electric potential energy per unit charge at a point in space. It provides a way to describe electric fields in terms of energy rather than force.
What is Electric Potential?
Electric potential is defined as the electric potential energy per unit test charge. It depends only on the source charge and distance, not on the test charge used to measure it.
- V: Electric potential (V = J/C)
- U: Electric potential energy (J)
- q₀: Test charge (C)
- k: Coulomb's constant = 8.99 × 10⁹ N⋅m²/C²
- q: Source charge (C)
- r: Distance from source charge (m)
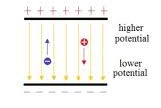
Relationship to Electric Potential Energy
Key Relationship
Electric potential energy equals the product of electric potential and charge:
$$U = qV$$
This relationship shows that:
- Electric potential is a property of the field (independent of test charge)
- Electric potential energy depends on both the field and the test charge
- Positive potential means positive test charges gain energy
- Negative potential means positive test charges lose energy
Sign of Electric Potential
Potential Sign Rules
- Positive potential: Due to positive source charges
- Negative potential: Due to negative source charges
- Zero potential: At infinite distance from any charge
- Reference point: Usually taken as infinity (V = 0)
Multiple Charge Systems
For multiple source charges, the total electric potential is the scalar sum of the individual potentials. This is much simpler than vector addition for electric fields.
Example: Two Charges
For two charges q₁ and q₂ at distances r₁ and r₂:
$$V = k\left(\frac{q_1}{r_1} + \frac{q_2}{r_2}\right)$$
Worked Examples
Example 1: Electric Potential Due to a Point Charge
Problem: Calculate the electric potential 3.0 m from a point charge of +4.0 μC.
Solution Steps:
- Given: q = +4.0 × 10⁻⁶ C, r = 3.0 m
- Formula: \(V = k\frac{q}{r}\)
- Substitute: \(V = (8.99 \times 10^9) \frac{4.0 \times 10^{-6}}{3.0}\)
- Calculate: \(V = 1.2 \times 10^4 \text{ V}\)
Answer: The electric potential is 1.2 × 10⁴ V (positive because the source charge is positive).
Example 2: Electric Potential Due to Multiple Charges
Problem: Two charges, +2.0 μC and -1.0 μC, are placed at (0,0) and (2,0) respectively. Find the electric potential at point (1,0).
Solution Steps:
- Distance to +2.0 μC: r₁ = 1.0 m
- Distance to -1.0 μC: r₂ = 1.0 m
- Potential from +2.0 μC: \(V_1 = k\frac{2.0 \times 10^{-6}}{1.0} = 1.8 \times 10^4 \text{ V}\)
- Potential from -1.0 μC: \(V_2 = k\frac{-1.0 \times 10^{-6}}{1.0} = -9.0 \times 10^3 \text{ V}\)
- Total potential: \(V = V_1 + V_2 = 9.0 \times 10^3 \text{ V}\)
Answer: The electric potential at (1,0) is 9.0 × 10³ V.
Example 3: Electric Potential Energy from Electric Potential
Problem: A charge of +3.0 μC is placed at a point where the electric potential is +5.0 × 10³ V. What is the electric potential energy of this charge?
Solution Steps:
- Given: q = +3.0 × 10⁻⁶ C, V = +5.0 × 10³ V
- Formula: \(U = qV\)
- Substitute: \(U = (+3.0 \times 10^{-6})(+5.0 \times 10^3)\)
- Calculate: \(U = 1.5 \times 10^{-2} \text{ J}\)
Answer: The electric potential energy is 1.5 × 10⁻² J (positive because both q and V are positive).
Electric Potential vs. Electric Field
Relationship
Electric field is the negative gradient of electric potential:
$$\vec{E_x} = -\frac{dV}{dx}$$
$$ \Delta V(x) = -\int \vec{E}_x \, dx $$
This relationship means:
- Electric field points in the direction of decreasing potential
- Stronger fields correspond to steeper potential gradients
- Uniform fields correspond to linear potential changes
- Zero field corresponds to constant potential
Applications of Electric Potential
- Circuit analysis: Electric potential differences drive current flow
- Particle accelerators: High potential differences accelerate charged particles
- Capacitors: Potential difference between plates stores energy
- Electron microscopes: High potentials focus electron beams
- Lightning: Large potential differences cause electrical breakdown
Practice Problems
Practice Problem 1
Problem: A charge of -2.0 μC creates an electric potential of -1.0 × 10⁴ V at a certain point. What is the distance from the charge to this point?
Click for solution
Solution:
- Given: V = -1.0 × 10⁴ V, q = -2.0 × 10⁻⁶ C
- Formula: \(r = k\frac{q}{V}\)
- Substitute: \(r = (8.99 \times 10^9) \frac{-2.0 \times 10^{-6}}{-1.0 \times 10^4}\)
- Calculate: \(r = 1.8 \text{ m}\)
Answer: 1.8 m
Practice Problem 2
Problem: Three charges are placed at the corners of an equilateral triangle: +1.0 μC, +2.0 μC, and -1.0 μC. The side length is 2.0 m. Find the electric potential at the center of the triangle.
Click for solution
Solution:
- Distance to center: \(r = \frac{2.0}{\sqrt{3}} = 1.15 \text{ m}\)
- Potential from each charge: \(V_i = k\frac{q_i}{r}\)
- Total potential: \(V = k\frac{1.0 \times 10^{-6} + 2.0 \times 10^{-6} - 1.0 \times 10^{-6}}{1.15}\)
- Result: \(V = 1.6 \times 10^4 \text{ V}\)
Answer: 1.6 × 10⁴ V
Key Concepts Summary
- Electric potential is energy per unit charge
- It's a scalar quantity (easier to work with than electric field)
- Positive potential means positive charges gain energy
- Negative potential means positive charges lose energy
- Potential is additive for multiple charges
- Electric field points from high to low potential
📝 Important Note
Electric potential is often called "voltage" in practical applications, especially in circuits. We'll explore this connection when we study electric circuits and current flow.
Quick Reference
- Single charge: \(V = k\frac{q}{r}\)
- Multiple charges: \(V = k\sum_{i} \frac{q_i}{r_i}\)
- Potential energy: \(U = qV\)
- Electric field: \(E = -\frac{dV}{dx}\)
- Units: V = J/C (Volts)