← Back to Concepts

Kirchhoff's Laws (KVL and KCL)

Kirchhoff's Laws are fundamental principles for analyzing complex electrical circuits. Kirchhoff's Voltage Law (KVL) states that the sum of voltages around any closed loop equals zero, while Kirchhoff's Current Law (KCL) states that the sum of currents entering a junction equals the sum of currents leaving it.

Kirchhoff's Voltage Law (KVL)

$$\sum V = 0$$

Kirchhoff's Voltage Law states that the algebraic sum of all voltage drops around any closed loop in a circuit equals zero. This means that the sum of voltage rises equals the sum of voltage drops.

🎯 KVL Statement

Around any closed loop in a circuit, the algebraic sum of all voltage drops equals zero.

This means: Sum of voltage rises = Sum of voltage drops

Sign Conventions for KVL

📏 KVL Sign Convention Rules

Choose Direction: Pick a direction to traverse the loop
Voltage Rise (+): When moving from - to + terminal of battery
Voltage Drop (-): When moving from + to - terminal of battery
Resistor Drop (-): When moving in direction of current through resistor
Resistor Rise (+): When moving against direction of current through resistor

Example: KVL in Simple Loop

Problem: Find the current in a circuit with a 12V battery and two resistors (3Ω, 6Ω) in series.

diagram — Simple loop with series resistors

Step 1: Choose Loop Direction

Let's traverse the loop clockwise.

Step 2: Write KVL Equation

$$V - I_1R_1 - I_2R_2 = 0$$

$$I_1 = I_2 = I$$

$$+12V - 3I - 6I = 0$$

Explanation:

+12V: Voltage rise across battery (moving from - to +)
-3I: Voltage drop across first resistor
-6I: Voltage drop across second resistor

Step 3: Solve for Current

$$12V - 9I = 0$$ $$9I = 12V$$ $$I = \frac{12V}{9Ω} = 1.33A$$

Answer

The current in the circuit is 1.33A.

Kirchhoff's Current Law (KCL)

$$\sum I_{in} = \sum I_{out}$$

Kirchhoff's Current Law states that the sum of currents entering a junction equals the sum of currents leaving the junction. This is based on the conservation of charge.

🎯 KCL Statement

At any junction in a circuit, the sum of currents entering equals the sum of currents leaving.

This means: Charge is conserved at every junction

Sign Conventions for KCL

📏 KCL Sign Convention Rules

Currents Entering (+): Currents flowing into the junction
Currents Leaving (-): Currents flowing out of the junction
Conservation: Total charge entering = Total charge leaving
Direction: Choose consistent direction for analysis

Example: KCL at Junction

Problem: Find the unknown current I₃ at a junction where I₁ = 2A (entering) and I₂ = 1.5A (leaving).

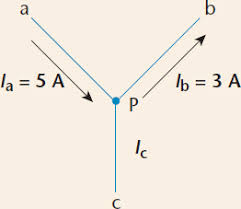
Step 1: Apply KCL

$$I_{in} = I_{out}$$ $$I_{in} = I_a$$ $$I_{out} = I_b+I_c$$

Step 2: Solve for Unknown Current

$$I_c = I_a-I_b$$ $$I_c = 5-3$$ $$I_c = 2$$

Answer

The current I_c is 2A (leaving the junction).

Combined Analysis

When analyzing complex circuits, both KVL and KCL are used together to create a system of equations that can be solved simultaneously.

This video helps to show to problem solving process:

This video is one of my favorites to understand how to solve these types of question:

Systematic Method

Identify loops and junctions
Assign current directions (arbitrary, but be consistent)
Write KVL equations for each independent loop
Write KCL equations for junctions (if needed)
Solve the system of equations

Key Takeaways

KVL: Conservation of energy - voltage rises equal voltage drops
KCL: Conservation of charge - current entering equals current leaving
Sign conventions are crucial for correct analysis
Independent loops are needed for KVL equations
Junctions provide additional constraints via KCL
Systematic approach prevents errors in complex circuits