← Back to Concepts

Kirchhoff's Voltage Law (KVL)

Kirchhoff's Voltage Law (KVL) is a fundamental principle in circuit analysis that states the sum of all voltage drops around any closed loop in a circuit must equal zero. This law is based on the conservation of energy and is essential for analyzing complex circuits.

Definition of KVL

$$\sum V = 0$$

Voltage drop from each resistor:

$$V_{drop} = iR$$

Kirchhoff's Voltage Law states that the algebraic sum of all voltage drops around any closed loop in a circuit equals zero. This means that the sum of voltage rises equals the sum of voltage drops.

Symbol: $\sum V = 0$
Units: Volts (V)
Principle: Conservation of energy
Application: Single-loop and multi-loop circuits

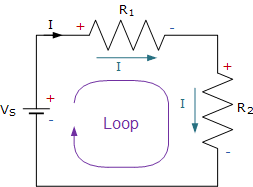
The loop starts from the negative terminal (0 V). It then jumps up by V_s and goes to R₁ where the voltage drops. Then it goes through the next resistor and voltage drops to 0. It then keeps going through the loop and when it reaches the battery it jumps back to V_s

Understanding KVL

Energy Conservation

Energy Source: Batteries and power supplies provide energy
Energy Consumption: Resistors and other components consume energy
Conservation: Energy gained = Energy lost
Voltage Representation: Voltage represents energy per unit charge

Physical Interpretation

Voltage Rise: Energy gained (batteries, power supplies)
Voltage Drop: Energy lost (resistors, loads)
Net Result: Total energy change around loop = 0
Direction: Choose a direction and stick to it consistently

🎯 KVL Statement

Around any closed loop in a circuit, the algebraic sum of all voltage drops equals zero.

This means: Sum of voltage rises = Sum of voltage drops

Sign Conventions for KVL

📏 Sign Convention Rules

Choose Direction: Pick a direction to traverse the loop
Voltage Rise (+): When moving from - to + terminal of battery
Voltage Drop (-): When moving from + to - terminal of battery
Resistor Drop (-): When moving in direction of current through resistor
Resistor Rise (+): When moving against direction of current through resistor

KVL Equation Formulation

Step-by-Step Process

Choose Loop Direction: Pick clockwise or counterclockwise
Identify Components: List all voltage sources and resistors
Assign Signs: Use sign convention for each component
Write Equation: Sum all voltages and set equal to zero
Solve: Use algebra to find unknown quantities

Example: Simple Single-Loop Circuit

Problem: Find the current in the circuit with a 12V battery and 6Ω resistor.

Step 1: Choose Loop Direction

Let's traverse the loop clockwise.

Step 2: Write KVL Equation

Starting from the battery and going clockwise:

$$+12V - I(6Ω) = 0$$

Explanation:

+12V: Voltage rise across battery (moving from - to +)
-I(6Ω): Voltage drop across resistor (moving in direction of current)
= 0: KVL requirement

Step 3: Solve for Current

$$12V - 6I = 0$$ $$6I = 12V$$ $$I = \frac{12V}{6Ω} = 2A$$

Answer

The current in the circuit is 2A.

KVL in Complex Circuits

Example: Multiple Voltage Sources

Problem: Find the current in a circuit with two batteries (12V and 6V) and a 3Ω resistor.

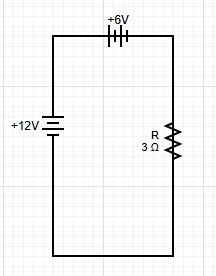
Step 1: Choose Loop Direction

Traverse clockwise starting from the 12V battery.

Step 2: Write KVL Equation

$$+12V - 6V - I(3Ω) = 0$$

Explanation:

+12V: Voltage rise across first battery
-6V: Voltage drop across second battery (opposing)
-I(3Ω): Voltage drop across resistor

Step 3: Solve for Current

$$12V - 6V - 3I = 0$$ $$6V - 3I = 0$$ $$3I = 6V$$ $$I = \frac{6V}{3Ω} = 2A$$

Answer

The current in the circuit is 2A.

KVL with Multiple Resistors

Example: Series Resistors

Problem: Find the current and voltage drops across each resistor in a circuit with a 9V battery and three resistors: 2Ω, 3Ω, and 4Ω in series.

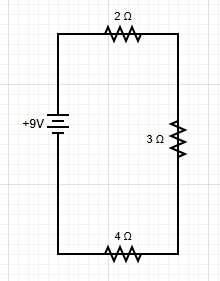
Step 1: Write KVL Equation

$$+9V - I(2Ω) - I(3Ω) - I(4Ω) = 0$$ $$+9V - I(2Ω + 3Ω + 4Ω) = 0$$ $$+9V - I(9Ω) = 0$$

Step 2: Solve for Current

$$9V - 9I = 0$$ $$9I = 9V$$ $$I = \frac{9V}{9Ω} = 1A$$

Step 3: Find Voltage Drops

$$V_1 = I \times R_1 = 1A \times 2Ω = 2V$$ $$V_2 = I \times R_2 = 1A \times 3Ω = 3V$$ $$V_3 = I \times R_3 = 1A \times 4Ω = 4V$$

Verification

$$V_{total} = V_1 + V_2 + V_3 = 2V + 3V + 4V = 9V$$

Answer

The current is 1A, and the voltage drops are 2V, 3V, and 4V respectively.

Common KVL Applications

🔋 Battery Circuits

Single Battery: V_battery - IR = 0
Series Batteries: V₁ + V₂ - IR = 0
Opposing Batteries: V₁ - V₂ - IR = 0

⚡ Resistor Networks

Series Resistors: V - I(R₁ + R₂ + R₃) = 0
Mixed Networks: Apply KVL to each loop
Complex Circuits: Use KVL with KCL for complete analysis

KVL vs. Ohm's Law

Relationship Between KVL and Ohm's Law

KVL: Conservation of energy around a loop

Ohm's Law: Relationship between voltage, current, and resistance

KVL Equation:

$$\sum V = 0$$

Ohm's Law:

$$V = IR$$

Combined:

$$\sum (IR) = \sum V_{sources}$$

Key Takeaways Summary

🎯 Essential KVL Concepts

Conservation: Energy is conserved around any closed loop
Sum to Zero: Algebraic sum of all voltages = 0
Direction Matters: Choose direction and stick to sign convention
Universal: Applies to any closed loop in any circuit

⚡ KVL Equation Steps

Choose Direction: Pick clockwise or counterclockwise
Identify Components: List all voltage sources and resistors
Assign Signs: Use sign convention consistently
Write Equation: Sum all voltages = 0
Solve: Use algebra to find unknowns

🔍 Sign Convention Rules

Battery Rise (+): Moving from - to + terminal
Battery Drop (-): Moving from + to - terminal
Resistor Drop (-): Moving in direction of current
Resistor Rise (+): Moving against direction of current

✅ Verification Methods

Energy Check: Total energy gained = Total energy lost
Voltage Check: Sum of voltage drops = Sum of voltage rises
Ohm's Law: V = IR must hold for each resistor
Power Check: Power supplied = Power dissipated

      💡 Pro Tips for KVL
      Be Consistent: Use the same direction throughout the loop
Check Signs: Verify sign assignments for each component
Start Simple: Begin with single-loop circuits
Practice Direction: Draw arrows to show your chosen direction
Verify Results: Always check that your answer makes sense

    