LC Circuits
Overview: Inductor-Capacitor Circuits
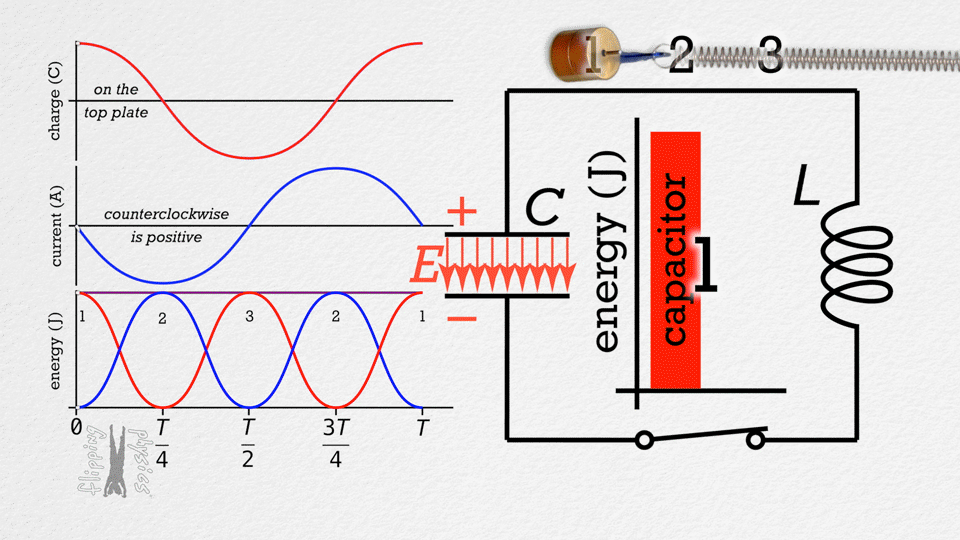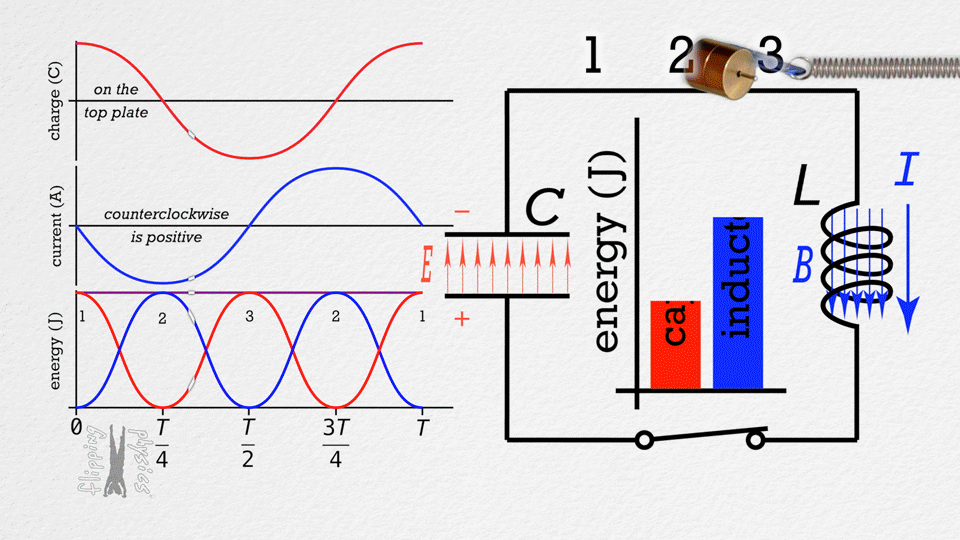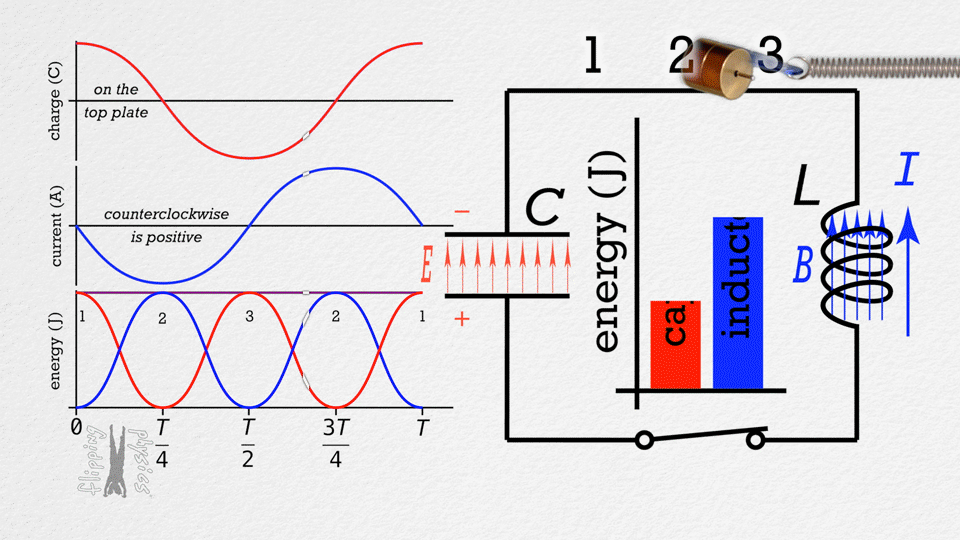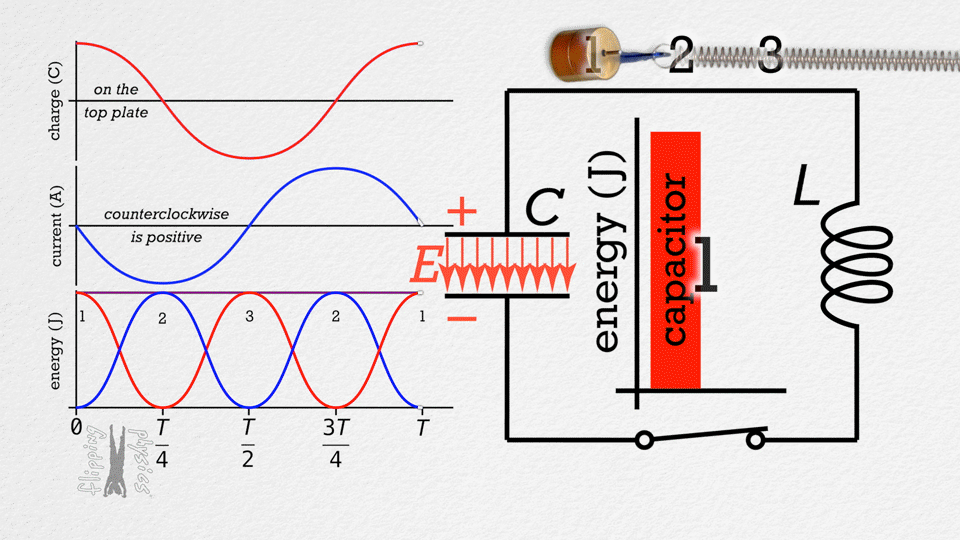
LC circuits consist of an inductor and capacitor connected together. When energy is stored in either component, it oscillates between the inductor's magnetic field and the capacitor's electric field. This creates electrical oscillations at a natural frequency determined by the inductance and capacitance.
These circuits are fundamental for understanding electrical oscillations, resonance, and are the basis for many electronic devices including radio tuners, filters, and oscillators.
Key Formulas
Natural Frequency
\[ f = \frac{1}{2\pi\sqrt{LC}} \]
Where:
- \(f\) is the natural frequency (Hz)
- \(L\) is the inductance (H)
- \(C\) is the capacitance (F)
Note: This formula is NOT on the AP Physics C equation sheet.
Angular Frequency
\[ \omega = \frac{1}{\sqrt{LC}} \]
Where:
- \(\omega\) is the angular frequency (rad/s)
- \(L\) is the inductance (H)
- \(C\) is the capacitance (F)
Note: This formula is NOT on the AP Physics C equation sheet.
Key Concepts
Energy Oscillation
Energy oscillates between:
- Capacitor: \(U_C = \frac{1}{2}CV^2\)
- Inductor: \(U_L = \frac{1}{2}LI^2\)
- Total energy is conserved
- When one is maximum, the other is zero
Current and Voltage
Current and voltage are 90° out of phase:
- When current is maximum, voltage is zero
- When voltage is maximum, current is zero
- Current leads voltage by 90°
Natural Frequency
The frequency depends on:
- Larger \(L\): lower frequency
- Larger \(C\): lower frequency
- Smaller \(L\) or \(C\): higher frequency
Applications
LC circuits are used in:
- Radio tuners
- Filters
- Oscillators
- Resonant circuits
Derivations (Not on AP Equation Sheet)
Derivation: Natural Frequency
Step-by-Step:
- Kirchhoff's voltage law: \(L\frac{dI}{dt} + \frac{Q}{C} = 0\)
- Since \(I = \frac{dQ}{dt}\), we get: \(L\frac{d^2Q}{dt^2} + \frac{Q}{C} = 0\)
- This is a second-order differential equation
- Solution: \(Q = Q_0\cos(\omega t)\) where \(\omega = \frac{1}{\sqrt{LC}}\)
- Frequency: \(f = \frac{\omega}{2\pi} = \frac{1}{2\pi\sqrt{LC}}\)
Example Problems
Example 1: Natural Frequency
Problem: An LC circuit has \(L = 0.1\) H and \(C = 1\) μF. What is the natural frequency?
- \(f = \frac{1}{2\pi\sqrt{LC}} = \frac{1}{2\pi\sqrt{(0.1)(10^{-6})}}\)
- \(f = \frac{1}{2\pi\sqrt{10^{-7}}} = \frac{1}{2\pi \times 3.16 \times 10^{-4}}\)
- \(f = 503\) Hz
Answer: 503 Hz
Example 2: Angular Frequency
Problem: What is the angular frequency for the above circuit?
- \(\omega = \frac{1}{\sqrt{LC}} = \frac{1}{\sqrt{(0.1)(10^{-6})}}\)
- \(\omega = \frac{1}{\sqrt{10^{-7}}} = 3162\) rad/s
Answer: 3162 rad/s
Example 3: Energy Oscillation
Problem: If the maximum voltage across the capacitor is 10 V, what is the maximum current in the inductor?
- Maximum capacitor energy: \(U_C = \frac{1}{2}CV^2 = \frac{1}{2}(10^{-6})(10)^2 = 5 \times 10^{-5}\) J
- Maximum inductor energy: \(U_L = \frac{1}{2}LI^2 = 5 \times 10^{-5}\) J
- \(I = \sqrt{\frac{2U_L}{L}} = \sqrt{\frac{2(5 \times 10^{-5})}{0.1}} = 0.032\) A
Answer: 0.032 A
One to watch:
Quiz: LC Circuits
1. What is the natural frequency for \(L = 0.2\) H and \(C = 0.5\) μF?
2. In an LC circuit, when the capacitor voltage is maximum:
3. If you increase the inductance in an LC circuit:
4. The total energy in an LC circuit:
Learning Objectives
- Calculate natural frequency for LC circuits
- Understand energy oscillation between components
- Determine phase relationship between current and voltage
- Apply to resonant circuits and filters
Key Takeaways
- Energy oscillates between capacitor and inductor
- Natural frequency: \(f = \frac{1}{2\pi\sqrt{LC}}\)
- Current and voltage are 90° out of phase
- Total energy is conserved
LC Circuit Interactive Simulation
Explore how current and voltage oscillate in an LC circuit: