← Back to Concepts

Magnetic Force on Current-Carrying Wires

Current-carrying wires experience magnetic forces when placed in magnetic fields. This fundamental interaction is the basis for electric motors, galvanometers, and many other electromagnetic devices. Understanding these forces is crucial for analyzing electromagnetic systems.

The Magnetic Force on a Wire

⚡ Magnetic Force Formula

The magnetic force on a current-carrying wire is given by:

This force is perpendicular to both the current direction and the magnetic field.

$$\vec{F}_B = I\vec{L} \times \vec{B}$$

Variables in the Formula

I: Current in the wire (A)
L: Length of wire in the magnetic field (m)
B: Magnetic field strength (T)
θ: Angle between current direction and magnetic field direction

Key Characteristics

Magnitude: $F_B = ILB\sin\theta$ where θ is the angle between current and field
Direction: Perpendicular to both current and magnetic field (palm rule)
Right-Hand Rule: Point fingers in field direction, thumb in current direction, palm faces force direction
Dependence: Force depends on current, wire length, and field strength
Vector Nature: Force is a vector quantity with magnitude and direction

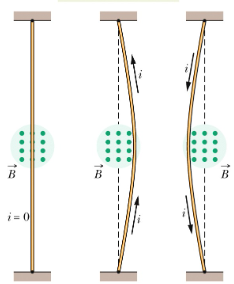
Vector diagram showing magnetic force perpendicular to current direction and magnetic field.

Example: Basic Wire Force Calculation

Problem: A 0.5 m wire carries 3 A of current perpendicular to a 0.2 T magnetic field. Calculate the magnetic force on the wire.

Step 1: Identify Given Values

Current: I = 3 A
Length: L = 0.5 m
Magnetic field: B = 0.2 T
Angle: θ = 90° (perpendicular)

Step 2: Apply Force Formula

$F_B = ILB\sin\theta$
$F_B = (3)(0.5)(0.2)\sin(90°)$
$F_B = 0.3$ N

Step 3: Determine Direction

Use right-hand rule: point fingers in magnetic field direction
Point thumb in current direction
Palm faces in force direction

Answer

The magnetic force is 0.3 N, directed perpendicular to both the current and magnetic field.

Why Magnetic Forces Arise from Current-Carrying Wires

🔍 Understanding the Source of Magnetic Forces

Magnetic forces on current-carrying wires arise from the collective motion of charged particles.

Each moving electron in the wire experiences a magnetic force, and these individual forces combine to create the net force on the wire.

Microscopic Explanation

Moving Electrons: Each electron in the wire moves with drift velocity
Individual Forces: Each electron experiences Lorentz force: $\vec{F} = q\vec{v} \times \vec{B}$
Collective Effect: All electron forces add up to create net force on wire
Wire Structure: Positive ions in wire lattice provide equal and opposite forces

Example: Force on Individual Electrons

Problem: Explain how the magnetic force on a wire relates to forces on individual electrons.

Step 1: Electron Motion

Electrons move with drift velocity through wire
Each electron has charge q = -1.6 × 10⁻¹⁹ C
Electrons move in direction opposite to conventional current

Step 2: Individual Forces

Each electron experiences: $\vec{F} = q\vec{v}_d \times \vec{B}$
Force direction depends on electron velocity and field
All electrons experience force in same direction

Step 3: Net Force

Total force = Sum of all individual electron forces
Net force = Number of electrons × Force per electron
This gives the macroscopic force formula: $\vec{F}_B = I\vec{L} \times \vec{B}$

Answer

The magnetic force on a wire is the sum of individual Lorentz forces on all moving electrons in the wire, resulting in the macroscopic force formula.

Electric Motor Principles

⚙️ Electric Motor Operation

Electric motors convert electrical energy to mechanical energy using magnetic forces on current-carrying wires.

The basic motor consists of a current-carrying coil in a magnetic field that experiences forces.

Motor Components

Armature: Current-carrying coil that experiences magnetic forces
Magnetic Field: Usually provided by permanent magnets or electromagnets
Commutator: Reverses current direction to maintain rotation
Brushes: Electrical contacts that connect to power source

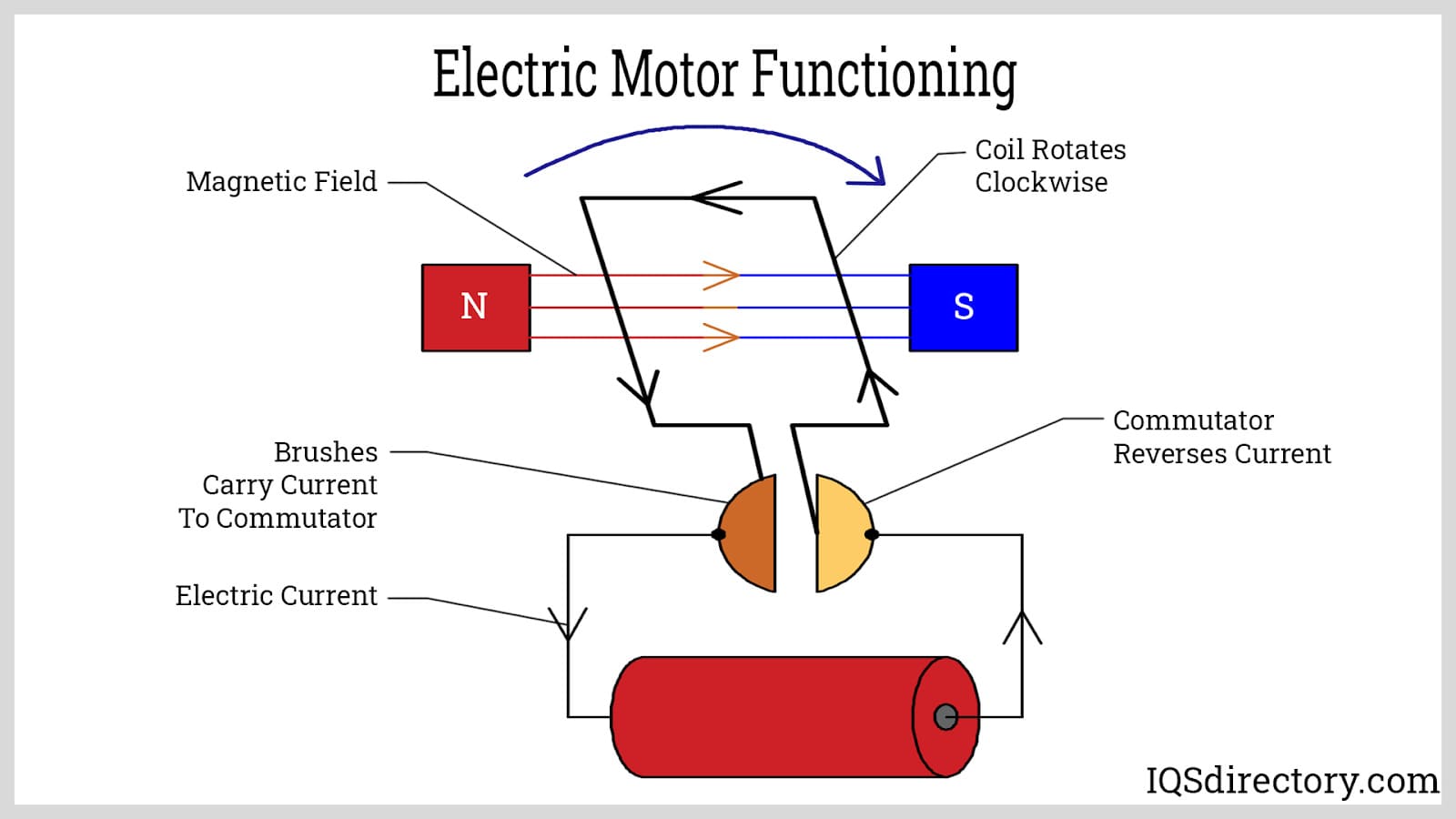
Simple electric motor showing armature, magnetic field, and commutator.

Example: Motor Force Calculation

Problem: A motor has 100 turns of wire, each with length 0.1 m, carrying 1 A in a 0.3 T field. Calculate the total magnetic force on the coil.

Step 1: Calculate Total Wire Length

Single turn length: L₁ = 0.1 m
Total length: (L_total) = N × L₁ = (100)(0.1) = 10 m

Step 2: Calculate Magnetic Force

$F_B = ILB\sin\theta$
$F_B = (1)(10)(0.3)\sin(90°)$
$F_B = 3$ N

Step 3: Motor Operation

Force causes coil to move
Commutator reverses current to maintain motion
Converts electrical energy to mechanical motion

Answer

The motor experiences a total magnetic force of 3 N on the coil, causing rotation and converting electrical to mechanical energy.

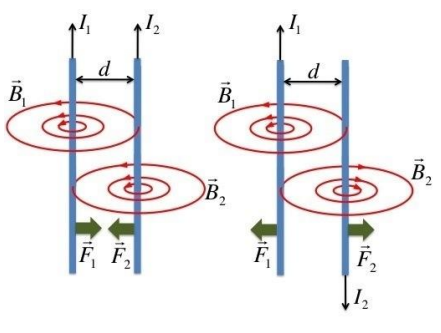
Force Between Parallel Wires

Mutual Magnetic Forces

Parallel Currents: Wires attract each other
Antiparallel Currents: Wires repel each other
Force per Unit Length: $\frac{F}{L} = \frac{\mu_0 I_1 I_2}{2\pi d}$
Distance Dependence: Force decreases with wire separation

$$\frac{F}{L} = \frac{\mu_0 I_1 I_2}{2\pi d}$$

Derivation of the Force Between Parallel Wires

🔬 Step-by-Step Derivation (come back after learning Ampere's law)

We derive the force between two parallel wires by combining Ampere's law and the magnetic force formula.

This derivation shows how the magnetic field from one wire creates a force on the other wire.

Magnetic Field from Wire 1

Using Ampere's law, the magnetic field at a distance d from a long straight wire carrying current I₁ is:

$$B_1 = \frac{\mu_0 I_1}{2\pi d}$$

Force on Wire 2

Wire 2, carrying current I₂, experiences a magnetic force due to the field B₁ from wire 1:

$$F_2 = I_2 L B_1sin\theta$$

Since the current in wire 2s perpendicular to the magnetic field from wire 1, θ = 90° and sin(90 = 1:

$$F_2 = I_2 L B_1$$

Step 3: Substitute the Magnetic Field

Substituting the expression for B₁ from Step 1:

$$F_2 = I_2 L \left(\frac{\mu_0 I_1}{2\pi d}\right)$$

$$F_2 = \frac{\mu_0 I_1 I_2}{2\pi d}$$

Step 4: Divide per Unit Length

Dividing both sides by L to get the force per unit length:

$$\frac{F_2}{L} = \frac{\mu_0 I_1 I_2}{2\pi d}$$

Step 5: Direction of Force

Parallel Currents (same direction): Wires attract each other
Antiparallel Currents (opposite directions): Wires repel each other
Right-Hand Rule: Use to determine force direction

Two parallel current-carrying wires experiencing mutual magnetic forces.

Example: Force Between Wires

Problem: Two parallel wires carry 5 A and 3 A in the same direction, separated by 0.1 m. Calculate the force per unit length.

Step 1: Identify Given Values

Current 1: I₁ = 5 A
Current 2: I₂ = 3 A
Separation: d = 0.1 m
Same direction: attractive force

Step 2: Apply Force Formula

$\frac{F}{L} = \frac{\mu_0 I_1 I_2}{2\pi d}$
$\frac{F}{L} = \frac{(4\pi \times 10^{-7})(5)(3)}{2\pi(0.1)}$
$\frac{F}{L} = 3 \times 10^{-5}$ N/m

Step 3: Determine Direction

Same current direction: attractive force
Wires are pulled toward each other

Answer

The force per unit length is 3 × 10⁻⁵ N/m, attracting the wires toward each other.

Practical Applications

🔧 Real-World Applications

Magnetic forces on current-carrying wires have numerous practical applications in modern technology.

These applications range from electric motors to precision measurement devices.

Key Applications

Electric Motors: Convert electrical energy to mechanical motion
Galvanometers: Measure small currents and voltages
Loudspeakers: Convert electrical signals to sound
Magnetic Levitation: Maglev trains use magnetic forces for propulsion
Circuit Breakers: Use magnetic forces to trip when current is too high
Electric Meters: Measure power consumption in homes

Example: Loudspeaker Operation

Problem: Explain how a loudspeaker uses magnetic forces on current-carrying wires.

Step 1: Voice Coil

Coil of wire attached to speaker cone
Carries audio signal current
Located in permanent magnetic field

Step 2: Magnetic Force

Current creates magnetic force on coil
Force direction depends on current direction
Force magnitude depends on current magnitude

Step 3: Sound Production

Coil moves back and forth with audio signal
Speaker cone moves with coil
Creates sound waves in air

Answer

The loudspeaker uses magnetic forces on the voice coil to convert electrical audio signals into mechanical motion, producing sound waves.

⚠️ Common Misconceptions

Force direction: Always perpendicular to both current and field, not parallel
Torque direction: Tends to align magnetic moment with field direction
Wire length: Only the component of length perpendicular to field matters
Current direction: Conventional current direction, not electron flow
Field strength: Force is proportional to field strength, not field direction

Key Takeaways

Force Formula: $\vec{F}_B = I\vec{L} \times \vec{B}$ for magnetic force on wires
Electron Motion: Forces arise from individual Lorentz forces on moving electrons
Electric Motors: Convert electrical to mechanical energy using magnetic forces
Galvanometers: Measure currents using balance of magnetic and restoring forces
Parallel Wires: Attract when currents are parallel, repel when antiparallel
Palm Rule: Point fingers in field direction, thumb in current direction, palm faces force direction
Applications: Used in motors, speakers, meters, and many other devices
Energy Conversion: Magnetic forces enable electrical-to-mechanical energy conversion