Multi-Loop Circuit Analysis

Multi-loop circuit analysis involves applying Kirchhoff's Laws systematically to solve complex circuits with multiple loops and junctions. This method allows us to find currents, voltages, and power in each component of the circuit.

Systematic Analysis Method

Step 1: Identify Circuit Elements

• Count the number of independent loops
• Identify all voltage sources (batteries, emf)
• Identify all resistors and their values
• Mark junctions where currents split or combine

Step 2: Assign Current Variables

• Assign a current variable to each independent loop
• Use consistent direction (clockwise or counterclockwise)
• Label currents as I₁, I₂, I₃, etc.
• Shared elements carry the difference of loop currents

Step 3: Apply Kirchhoff's Voltage Law

• Write KVL equation for each independent loop
• Follow sign conventions: +V for voltage rises, -V for drops
• Include all voltage sources and resistors in each loop
• For shared elements, use the net current through them

Step 4: Apply Kirchhoff's Current Law (if needed)

• Use KCL at junctions to relate loop currents
• This provides additional equations if needed
• Often not necessary if loop currents are independent

Step 5: Solve the System of Equations

• Use substitution, elimination, or matrix methods
• Check that the number of equations equals the number of unknowns
• Verify solutions by checking power conservation

Example: Three-Loop Circuit

Problem: Find the currents in a circuit with three loops, multiple resistors, and two batteries (12 V and 3 V).

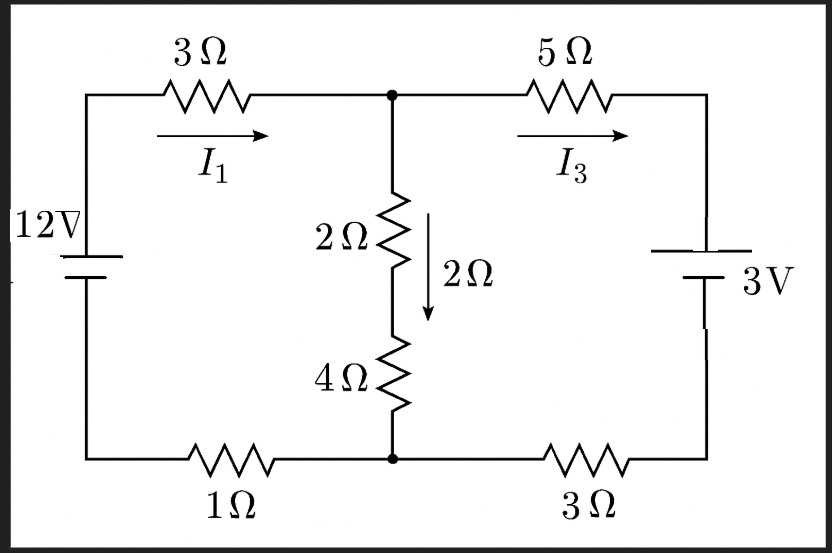
Step 1: Assign Current Variables

Let \( I_1 \) be the current in the left loop (clockwise), \( I_2 \) be the current through the middle vertical branch (downward), and \( I_3 \) be the current in the right loop (clockwise).

Step 2: Write KVL Equations

Apply Kirchhoff’s Voltage Law (KVL) to each loop, using the passive sign convention and Ohm’s Law.

$$\text{Loop 1 (left loop): } 12 - 3I_1 - 2(I_1 - I_2) - 1I_1 = 0$$ $$\text{Loop 2 (vertical middle branch): } 2(I_1 - I_2) + 4I_2 - 2(I_3 - I_2) = 0$$ $$\text{Loop 3 (right loop): } 5I_3 + 2(I_3 - I_2) + 3I_3 - 3 = 0$$

Step 3: Simplify the Equations

$$\text{Loop 1: } 12 = 6I_1 - 2I_2$$ $$\text{Loop 2: } 0 = 2I_1 - 8I_2 + 2I_3$$ $$\text{Loop 3: } 3 = 10I_3 - 2I_2$$

Step 4: Solve the System of Equations

Solving this system (by substitution or matrix methods) gives:

$$I_1 = \frac{231}{104} \approx 2.22\,\text{A}$$ $$I_2 = \frac{69}{104} \approx 0.66\,\text{A}$$ $$I_3 = \frac{45}{104} \approx 0.43\,\text{A}$$

Answer

The currents are:

• \( I_1 = \frac{231}{104} \approx 2.22\,\text{A} \) (left loop, clockwise)
• \( I_2 = \frac{69}{104} \approx 0.66\,\text{A} \) (middle branch, downward)
• \( I_3 = \frac{45}{104} \approx 0.43\,\text{A} \) (right loop, clockwise)

Common Circuit Patterns

Bridge Circuits

Circuits with cross-connections require careful current assignment:

• Use mesh analysis (loop currents)
• Identify independent loops carefully
• Shared elements carry current differences

Delta-Wye Transformations

For complex resistor networks:

• Convert delta (Δ) to wye (Y) configurations
• Simplify before applying KVL/KCL
• Transform back to find individual currents

Superposition Method

For circuits with multiple sources:

• Analyze each source separately
• Set other sources to zero (replace batteries with wires)
• Add results algebraically

Power Analysis

Verification

• Check that power supplied equals power dissipated
• Verify that currents satisfy KCL at all junctions
• Confirm that voltage drops satisfy KVL around all loops

Power Analysis

Verification

• Check that power supplied equals power dissipated
• Verify that currents satisfy KCL at all junctions
• Confirm that voltage drops satisfy KVL around all loops

For More Explanation/Practice:

Key Takeaways

• Systematic approach prevents errors in complex circuits
• Independent loops are crucial for correct analysis
• Sign conventions must be consistent throughout
• Power conservation provides a verification method
• Practice with various circuit topologies builds intuition
• Matrix methods are efficient for complex systems