RC Circuits and Transient Behavior
RC circuits consist of resistors and capacitors connected together. These circuits exhibit transient behavior, meaning their voltage and current change over time when the circuit is switched on or off. Understanding RC circuits is crucial for analyzing timing circuits, filters, and energy storage systems.
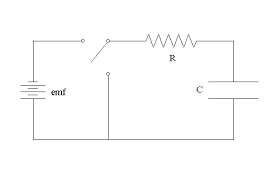
Time Constant
🎯 Time Constant Definition
The time constant τ (tau) determines how quickly an RC circuit responds to changes.
It represents the time required for the voltage or current to change by 63.2% of its total change.
The time constant is the product of resistance and capacitance. It has units of seconds and characterizes the speed of the circuit's response to changes.
Physical Interpretation
- Small τ: Fast response, quick charging/discharging
- Large τ: Slow response, gradual charging/discharging
- 5τ Rule: After 5 time constants, the circuit reaches 99.3% of its final value
- Units: τ = (ohms) × (farads) = seconds

Example: Calculating Time Constant
Problem: Find the time constant of an RC circuit with R = 10kΩ and C = 100μF.
Step 1: Use Time Constant Formula
Step 2: Convert Units
Answer
The time constant is 1 second.
Mathematical Derivation
Differential Equation for RC Circuit
For an RC circuit with battery voltage V₀, we can write Kirchhoff's voltage law:
Since I = dQ/dt, we get the differential equation:
Rearranging:
This is a first-order linear differential equation with solution:
Deriving V(t) from Q(t)
Since V = Q/C:
With τ = RC:
Deriving I(t) from Q(t)
Since I = dQ/dt:
Using the chain rule:
With τ = RC:
Charging Process
⚡ Charging Behavior
When a capacitor charges, voltage increases exponentially toward the battery voltage.
Current decreases exponentially as the capacitor fills up.
Voltage During Charging
Current During Charging
During charging, the capacitor voltage starts at zero and approaches the battery voltage exponentially. The current starts at its maximum value and decreases exponentially to zero.
Example: Charging Analysis
Problem: In an RC circuit with τ = 2s and V₀ = 12V, find the capacitor voltage after 4 seconds.
Step 1: Use Charging Formula
Step 2: Calculate Exponential
Answer
The capacitor voltage is 10.38V after 4 seconds.
Discharging Process
Differential Equation for Discharging
When the switch opens, the battery is disconnected. Kirchhoff's voltage law becomes:
Since I = dQ/dt:
Rearranging:
This is a first-order linear differential equation with solution:
Where Q₀ is the initial charge on the capacitor.
Deriving V(t) for Discharging
Since V = Q/C and Q₀ = CV₀:
With τ = RC:
Deriving I(t) for Discharging
Since I = dQ/dt:
Using the chain rule:
Since Q₀ = CV₀:
With τ = RC:
The negative sign indicates current flows in the opposite direction during discharging.
🎯 Discharging Behavior
When a capacitor discharges, voltage decreases exponentially toward zero.
Current also decreases exponentially but flows in the opposite direction.
Voltage During Discharging
Current During Discharging
During discharging, the capacitor voltage starts at its initial value and decreases exponentially to zero. The current flows in the opposite direction and also decreases exponentially.
Example: Discharging Analysis
Problem: A capacitor initially charged to 9V discharges through a resistor. If τ = 3s, find the voltage after 6 seconds.
Step 1: Use Discharging Formula
Step 2: Calculate Exponential
Answer
The capacitor voltage is 1.22V after 6 seconds.
Key Time Points
Important Time Intervals
- t = τ: 63.2% of total change (charging: 63.2% of V₀, discharging: 36.8% of V₀)
- t = 2τ: 86.5% of total change
- t = 3τ: 95.0% of total change
- t = 5τ: 99.3% of total change (practically complete)
Example: Time Point Analysis
Problem: A 10V capacitor discharges with τ = 1s. Find the voltage at t = 2τ.
Step 1: Calculate Time
Step 2: Use Discharging Formula
Verification
At t = 2τ, the voltage should be 13.5% of the initial value, which matches our calculation.
Answer
The voltage is 1.35V at t = 2τ.
This video really helps sum everything up:
Interactive RC Circuit Simulation
RC Circuit Parameters
Circuit Values
Time Constant (τ): 1.0s
Capacitor Voltage: 0.0V
Current: 0.0mA
Time Elapsed: 0.0s
Status: Ready
Real-time Graphs
Voltage vs Time
Current vs Time
Charge vs Time
Key Takeaways
- Time Constant: τ = RC determines circuit response speed
- Charging: Voltage increases exponentially, current decreases
- Discharging: Voltage decreases exponentially, current reverses
- 5τ Rule: Circuit reaches 99.3% of final value after 5τ
- Exponential Behavior: All RC circuit responses follow exponential functions
- Practical Importance: Essential for timing, filtering, and energy applications