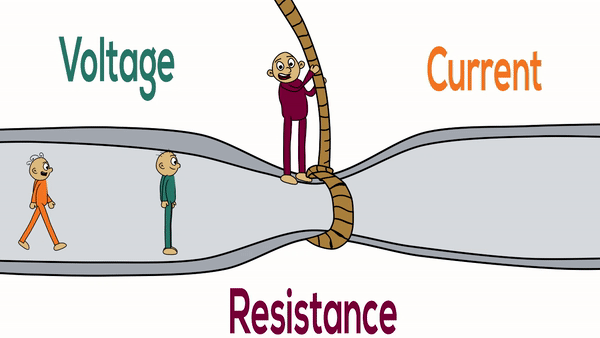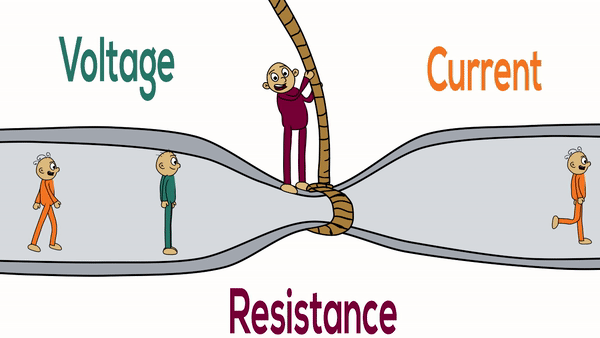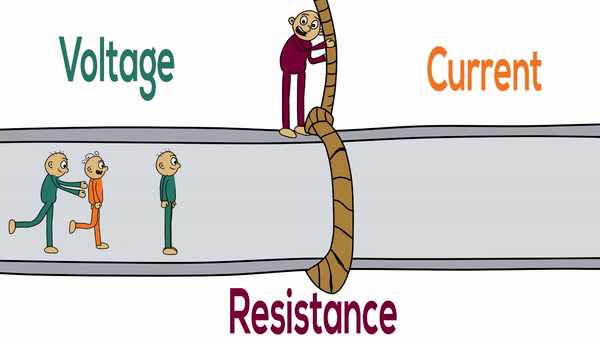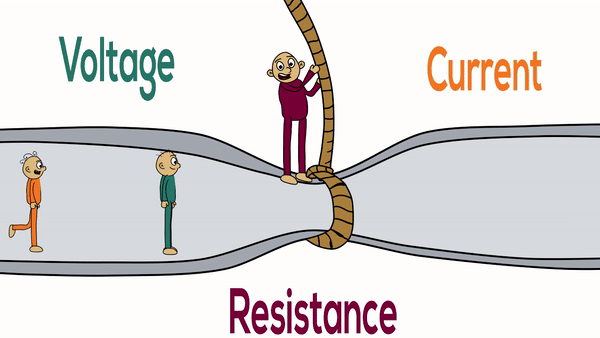
Electrical Resistance
Electrical resistance is a fundamental property of materials that opposes the flow of electric current. Understanding resistance is crucial for analyzing electrical circuits, designing electronic devices, and predicting how materials will behave in electrical applications.
Definition of Resistance
Resistance is defined as the ratio of voltage across a conductor to the current flowing through it. It measures how much a material opposes the flow of electric charge.
- Units: Ohms (Ω)
- Symbol: \(R\)
- Definition: Opposition to current flow

Resistivity and Resistance
The resistance of a conductor depends on its material properties (resistivity) and geometry (length and cross-sectional area).
- Where:
- \(R\) = resistance (Ω)
- \(\rho\) = resistivity (Ω·m)
- \(L\) = length (m)
- \(A\) = cross-sectional area (m²)
- Material property: Resistivity depends on the material
- Geometric factors: Length and area affect resistance
- Temperature dependence: Resistivity changes with temperature
Factors Affecting Resistance
Material (Resistivity)
- Conductors: Low resistivity (copper: 1.68 × 10⁻⁸ Ω·m)
- Insulators: High resistivity (glass: ~10¹² Ω·m)
- Semiconductors: Intermediate resistivity (silicon: ~10³ Ω·m)
- Superconductors: Zero resistivity below critical temperature
Length
- Direct proportionality: \(R \propto L\)
- Longer wire: Higher resistance
- Shorter wire: Lower resistance
- Linear relationship: Double length = double resistance
Cross-Sectional Area
- Inverse proportionality: \(R \propto \frac{1}{A}\)
- Thicker wire: Lower resistance
- Thinner wire: Higher resistance
- Area relationship: Double area = half resistance
Temperature
- Metals: Resistance increases with temperature
- Semiconductors: Resistance decreases with temperature
- Superconductors: Zero resistance below critical temperature
Memory Trick: RLA Formula
Remember the resistance formula using RLA:
- R = Resistance (what we're calculating)
- L = Length (longer = more resistance)
- A = Area (larger = less resistance)
So: \(R = \rho \frac{L}{A}\)
Think: Resistance = resistivity × (length ÷ area)
This helps you remember that resistance increases with length and decreases with area!
Short Circuits
A short circuit occurs when a low-resistance path is created between two points in a circuit, bypassing the intended load. This creates a very high current flow that can damage components and pose safety hazards.
What is a Short Circuit?
- Definition: A path of very low resistance between two points in a circuit
- Resistance: Approaches zero (R ≈ 0 Ω)
- Current: Becomes very large (I = V/R → ∞ as R → 0)
- Voltage: Drops to nearly zero across the short
Effects of Short Circuits
- High current: Can exceed component ratings
- Heat generation: \(P = I^2R\) becomes very large
- Component damage: Wires can melt, components can burn
- Fire hazard: Excessive heat can cause fires
- Circuit failure: Normal operation stops
Protection Against Short Circuits
- Fuses: Melt when current exceeds rating
- Circuit breakers: Automatically open when current is too high
- Current limiting: Resistors or other components that limit current
- Proper wiring: Insulation prevents accidental shorts
Example: Short Circuit Current
Problem: A 12 V battery is accidentally short-circuited with a wire of resistance 0.01 Ω. What current flows?
Solution:
- Ohm's Law: \(I = \frac{V}{R}\)
- Substitution: \(I = \frac{12 \text{ V}}{0.01 \text{ Ω}}\)
- Calculation: \(I = 1200 \text{ A}\)
Answer: The current is 1200 A, which is extremely dangerous!
Note: This is why fuses and circuit breakers are essential safety devices.
Resistance in Series and Parallel
Series Resistance
- Current: Same through all resistors
- Voltage: Divides across resistors
- Total resistance: Sum of individual resistances
- Power: \(P = I^2R_{total}\)
Parallel Resistance
- Voltage: Same across all resistors
- Current: Divides through resistors
- Total resistance: Less than smallest individual resistance
- Power: \(P = \frac{V^2}{R_{total}}\)
Worked Examples
Interactive Resistance Simulation
Explore how resistance changes with wire length and cross-sectional area:
Example 1: Basic Resistance Calculation
Problem: A copper wire is 10.0 m long and has a diameter of 2.0 mm. If copper has resistivity 1.68 × 10⁻⁸ Ω·m, what is the resistance of the wire?
Solution:
- Cross-sectional area: \(A = \pi r^2 = \pi(1.0 \times 10^{-3})^2 = 3.14 \times 10^{-6} \text{ m}^2\)
- Resistance formula: \(R = \rho \frac{L}{A}\)
- Substitution: \(R = (1.68 \times 10^{-8}) \frac{10.0}{3.14 \times 10^{-6}}\)
- Calculation: \(R = 5.35 \times 10^{-2} \text{ Ω} = 0.0535 \text{ Ω}\)
Answer: The resistance is 0.0535 Ω.