← Back to Concepts

Single-Loop Circuit Analysis

Single-loop circuit analysis is the foundation of circuit theory. These circuits contain one complete path for current flow and can be analyzed using Kirchhoff's Voltage Law (KVL). Understanding single-loop analysis is essential for more complex multi-loop circuits.

What is a Single-Loop Circuit?

Single-Loop Circuit: A circuit that contains exactly one closed path for current flow. All components are connected in series, and the same current flows through every component.

Characteristics of single-loop circuits:

One Current: Same current flows through all components
Series Connection: All components are in series
KVL Analysis: One KVL equation is sufficient
Simple Solution: Direct application of Ohm's Law

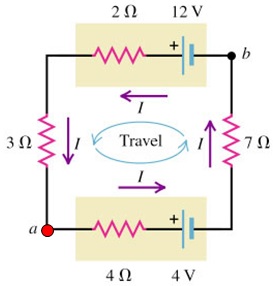
Single-loop circuit with batteries and resistors in series.

Systematic Analysis Method

Identify the Circuit

Confirm that the circuit has only one loop. All components should be connected in series with no branching.

💡 Tip: Trace the current path to ensure there's only one complete loop.

Choose Loop Direction

Pick a direction (clockwise or counterclockwise) to traverse the loop. This direction will be used for sign conventions.

        ⚡ Direction Rule: Be consistent with your chosen direction throughout the analysis.
      

Write KVL Equation

Apply Kirchhoff's Voltage Law around the loop. Sum all voltage rises and drops, setting the total equal to zero.

$$\sum V = 0$$

For single-loop circuits:

$$\sum V_{sources} - \sum IR = 0$$

⚡ KVL Rule: Voltage rises = Voltage drops around the loop.

Solve for Current

Use algebra to solve for the current. Since all components are in series, there's only one current value.

$$I = \frac{\sum V_{sources}}{\sum R}$$

✅ Result: One current value for the entire circuit.

Find Voltage Drops

Use Ohm's Law to find the voltage drop across each resistor: V = IR.

$$V_i = I \times R_i$$

✅ Verification: Sum of voltage drops should equal sum of voltage sources.

Worked Example: Basic Single-Loop Circuit

Example: Find current and voltage drops

Problem: A 24V battery is connected to three resistors in series: R₁=4Ω, R₂=6Ω, R₃=2Ω. Find the current and voltage drop across each resistor.

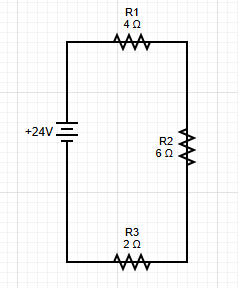
Single-loop circuit with three resistors

Step 1: Identify the Circuit

This is a single-loop circuit with one battery and three resistors in series.

Step 2: Choose Loop Direction

Let's traverse the loop clockwise, starting from the battery.

Step 3: Write KVL Equation

$$+24V - I(4Ω) - I(6Ω) - I(2Ω) = 0$$ $$+24V - I(4Ω + 6Ω + 2Ω) = 0$$ $$+24V - I(12Ω) = 0$$

Step 4: Solve for Current

$$24V - 12I = 0$$ $$12I = 24V$$ $$I = \frac{24V}{12Ω} = 2A$$

Step 5: Find Voltage Drops

$$V_1 = I \times R_1 = 2A \times 4Ω = 8V$$ $$V_2 = I \times R_2 = 2A \times 6Ω = 12V$$ $$V_3 = I \times R_3 = 2A \times 2Ω = 4V$$

Step 6: Verify Results

$$V_{total} = V_1 + V_2 + V_3 = 8V + 12V + 4V = 24V$$

Results Summary

Component	Resistance (Ω)	Current (A)	Voltage Drop (V)	Power (W)
R₁	4	2	8	16
R₂	6	2	12	24
R₃	2	2	4	8
Total	12	2	24	48

Answer

The current is 2A, and the voltage drops are 8V, 12V, and 4V respectively.

Complex Single-Loop Examples

Example: Multiple Voltage Sources

Problem: A circuit has two batteries (18V and 6V) and three resistors (3Ω, 4Ω, 5Ω) in series. Find the current and voltage drops.

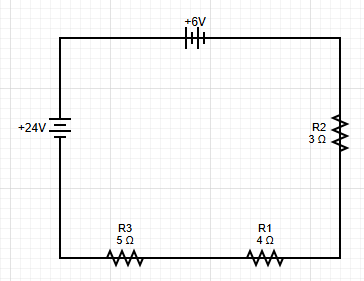
Single-loop circuit with multiple voltage sources

Step 1: Write KVL Equation

$$+18V - 6V - I(3Ω) - I(4Ω) - I(5Ω) = 0$$ $$+12V - I(12Ω) = 0$$

Remember: going from the positive to the negative terminal of the battery is a voltage drop.

Step 2: Solve for Current

$$12V - 12I = 0$$ $$I = \frac{12V}{12Ω} = 1A$$

Step 3: Find Voltage Drops

$$V_1 = 1A \times 3Ω = 3V$$ $$V_2 = 1A \times 4Ω = 4V$$ $$V_3 = 1A \times 5Ω = 5V$$

Answer

The current is 1A, and the voltage drops are 3V, 4V, and 5V respectively.

Common Single-Loop Configurations

🔋 Single Battery with Multiple Resistors

$$I = \frac{V_{battery}}{R_1 + R_2 + R_3 + ...}$$ $$V_i = I \times R_i$$

Application: Most common single-loop configuration

⚡ Multiple Batteries in Series

$$I = \frac{V_1 + V_2 + V_3 + ...}{R_1 + R_2 + R_3 + ...}$$

Application: Battery packs and voltage addition

🔄 Opposing Batteries

$$I = \frac{V_1 - V_2}{R_1 + R_2 + R_3 + ...}$$

Application: When batteries oppose each other

Power Analysis in Single-Loop Circuits

Power Calculations

In single-loop circuits, power can be calculated for each component:

Power Formulas

Resistor Power: P = I²R = V²/R = IV
Battery Power: P = IV (positive if supplying, negative if receiving)
Total Power: P_total = I²R_total

Example: Power Calculation

Using the previous example with I = 2A:

$$P_1 = I^2R_1 = (2A)^2 \times 4Ω = 16W$$ $$P_2 = I^2R_2 = (2A)^2 \times 6Ω = 24W$$ $$P_3 = I^2R_3 = (2A)^2 \times 2Ω = 8W$$ $$P_{total} = 16W + 24W + 8W = 48W$$

Key Takeaways Summary

🎯 Essential Single-Loop Concepts

One Current: Same current flows through all components
Series Connection: All components are in series
KVL Analysis: One equation is sufficient
Simple Solution: Direct application of Ohm's Law

⚡ Analysis Steps

Identify: Confirm single-loop configuration
Choose Direction: Pick clockwise or counterclockwise
Write KVL: Sum all voltages = 0
Solve Current: I = ΣV_sources / ΣR
Find Voltages: V_i = I × R_i

🔍 Key Formulas

Current: I = V_total / R_total
Voltage Drop: V_i = I × R_i
Power: P_i = I²R_i = V_i²/R_i
Verification: ΣV_drops = ΣV_sources

✅ Verification Methods

Voltage Check: Sum of voltage drops = battery voltage
Current Check: Same current through all components
Power Check: Power supplied = Power dissipated
Ohm's Law: V = IR must hold for each resistor

      💡 Pro Tips for Single-Loop Analysis
      Start Simple: Begin with basic single-battery circuits
Be Systematic: Follow the 5-step method consistently
Check Signs: Verify sign conventions for voltage sources
Verify Results: Always check that your answer makes sense
Practice Regularly: Single-loop analysis is the foundation for complex circuits

    