← Back to Concepts

Center of Mass and System Motion

The center of mass is the point where an object's mass is effectively concentrated for purposes of analyzing motion. It is a powerful simplification tool for analyzing systems of particles and extended bodies.

Defining the Center of Mass

In one dimension, for discrete masses, the center of mass is given by:

\[ x_{\text{cm}} = \frac{m_1x_1 + m_2x_2 + \cdots + m_nx_n}{m_1 + m_2 + \cdots + m_n} \]

In vector form for three dimensions:

\[ \vec{R}_{\text{cm}} = \frac{\sum m_i \vec{r}_i}{\sum m_i} \]

This formula holds for both particles and continuous mass distributions. For a rigid body, the center of mass is fixed relative to the body, while for systems of particles it may move dynamically.

System Motion and Newton’s Second Law

Applying Newton’s Second Law to a system of particles leads to a fundamental result:

\[ \vec{F}_{\text{net, external}} = M \vec{a}_{\text{cm}} \]

Here, \( M \) is the total mass of the system and \( \vec{a}_{\text{cm}} \) is the acceleration of the center of mass. Internal forces between parts of the system cancel due to Newton’s Third Law and do not affect the motion of the center of mass.

Conservation of Momentum and COM

If the net external force on a system is zero, the total momentum is conserved and the center of mass moves at constant velocity:

\[ \vec{v}_{\text{cm}} = \text{constant} \quad \text{(if } \vec{F}_{\text{ext}} = 0 \text{)} \]

Applications and Deeper Insights

Projectile Motion of Systems: For any system in free fall (like an object breaking apart midair), the center of mass follows a parabolic trajectory.
Explosions and Collisions: The internal explosion of a system (e.g. a firework) doesn’t change the motion of the center of mass. It still obeys conservation laws.
Variable Mass Systems: In rocket motion, although the rocket loses mass, we can still track the system's center of mass to understand its motion.
Torque and Rotation (covered in later unit): For torque calculations, the center of mass is the natural pivot for translation-rotation separation. Torque about the COM determines angular acceleration.
Stability: An object is stable if a vertical line from the COM lies within its base. This is crucial in biomechanics and structural engineering.

Don't believe me about projectile motion? Watch this:

Example: Object Breaking in Midair

Imagine a rock exploding into pieces while flying through the air. Each piece flies off in a different direction. Despite this, the COM of the system (all the fragments) still follows the original parabolic trajectory as if the explosion never occurred.

The blue ball signifies CoM.

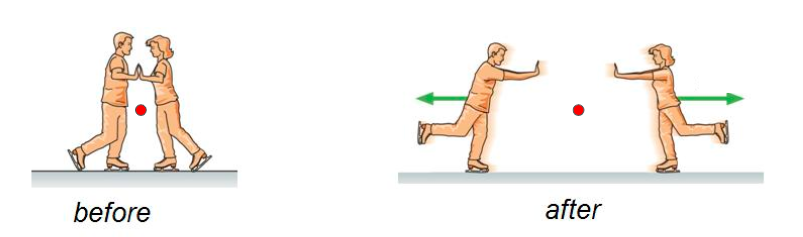
Example: Skaters Pushing Off

Consider two ice skaters at rest who push off each other. Even though they move in opposite directions, the center of mass of the system remains stationary because no external force acts horizontally.

Red dot is the center of mass of the system (the 2 figure skaters). Center of mass stays fixed in an isolated system with no net external force.

Example: A Rocket Launching

As a rocket ejects fuel downward, it loses mass. But the motion of the system (rocket + ejected fuel) still conserves total momentum. The COM accelerates smoothly even though the rocket’s mass changes continuously.

Rotating and Translating Objects

When analyzing objects that rotate and translate (e.g. rolling wheels), the translational motion of the COM is often separated from the rotational motion about the COM. This separation makes energy and force analysis much easier.

Practice Example 1: Two-Mass System

Problem: A 3 kg block is at position \( x = 0 \, \text{m} \), and a 5 kg block is at \( x = 4 \, \text{m} \). What is the position of the center of mass?

Solution:

\[ x_{\text{cm}} = \frac{m_1x_1 + m_2x_2}{m_1 + m_2} = \frac{3(0) + 5(4)}{3 + 5} = \frac{20}{8} = 2.5 \, \text{m} \]

Answer: The center of mass is at \( x = 2.5 \, \text{m} \).

Practice Example 2: Explosion Problem

Problem: A 6 kg object at rest explodes into two fragments. A 2 kg piece flies off to the left at 12 m/s. What is the velocity of the 4 kg piece so that the center of mass continues at rest?

Solution:

Use conservation of momentum. The total momentum before and after must be zero:

\[ m_1v_1 + m_2v_2 = 0 \quad \Rightarrow \quad 2(-12) + 4v = 0 \] \[ -24 + 4v = 0 \quad \Rightarrow \quad v = 6 \, \text{m/s} \]

Answer: The 4 kg piece must move at \( 6 \, \text{m/s} \) to the right.

Summary

The center of mass acts as a simplified model point for real-world objects and complex systems. Understanding the COM allows us to apply Newton’s laws, conservation laws, and rotational dynamics far more easily. Whether studying rockets, collisions, or rolling motion, tracking the COM turns a difficult system into a manageable physics problem.

2D Center of Mass Simulator

Enable Moving Objects

Object 1

Mass: Position X: Position Y:

Object 2

Mass: Position X: Position Y:

Center of Mass: