Explosions and Recoil
Key Concept
Explosions are reverse collisions: a single object breaks into multiple pieces. Even though there may be violent internal forces (like an explosion), the total momentum of the system remains conserved—if no external force acts on it.
System at Rest Before Explosion
If a system starts at rest, then total momentum is zero before the explosion (no velocity). After the explosion, the individual momenta of all parts must still sum to zero. Each part goes off in a different direction, but since momentum is a vector quantity, everything will sum to zero.
Example: Gun Recoil
When a bullet is fired, the gun recoils in the opposite direction. The chemical explosion of the gunpowder is an internal force within the gun-bullet system. According to Newton's 3rd Law, the bullet and gun exert equal and opposite forces on each other.

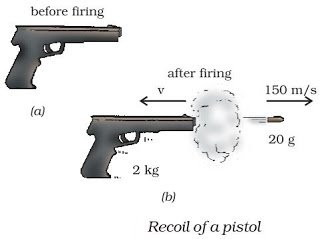
Example: Rocket Propulsion
Rockets move by expelling hot gas backward. The explosion inside the combustion chamber is also an internal force. Since the rocket starts at rest and no external forces act, the rocket gains forward momentum equal and opposite to the gas it expels.

2D Explosions
In two-dimensional explosions, you must conserve momentum in both the \( x \)- and \( y \)-directions:
Key Takeaways
- Total momentum is conserved if no net external force acts on the system.
- Internal forces like chemical explosions or springs cannot change total momentum.
- When starting at rest, final momentum of all pieces must add to zero.
- Gun recoil, rocket thrust, and fragment motion are all explained by conservation of momentum.
- Always use vector components in 2D problems.
Worked Examples
Problem: A 2.0 kg rifle fires a 0.020 kg bullet at 400 m/s. What is the recoil velocity of the rifle?
Solution:
Before firing, both are at rest: \( p_{\text{initial}} = 0 \)
After firing, by conservation of momentum: \[ 0 = m_b v_b + m_g v_g \\ 0 = (0.020)(400) + (2.0)v_g \\ 0 = 8 + 2.0v_g \\ v_g = -4.0 \text{ m/s} \] Answer: The rifle recoils at 4.0 m/s in the opposite direction to the bullet.
Problem: A 1000 kg rocket in deep space expels 10 kg of gas at 2000 m/s backward. What is the rocket's velocity after the gas is expelled, if it started at rest?
Solution:
Initial momentum: \( p_{\text{initial}} = 0 \)
After expelling gas: \[ 0 = m_r v_r + m_e v_e \\ 0 = (990)v_r + (10)(-2000) \\ 0 = 990v_r - 20000 \\ 990v_r = 20000 \\ v_r = \frac{20000}{990} \approx 20.2 \text{ m/s} \] Answer: The rocket moves forward at approximately 20.2 m/s.
Problem: A 3.0 kg object at rest explodes into two pieces: a 1.0 kg piece moves right at 6 m/s. What is the velocity of the 2.0 kg piece?
Solution:
Initial momentum: \( p_{\text{initial}} = 0 \)
After explosion: \[ 0 = m_1 v_1 + m_2 v_2 \\ 0 = (1.0)(6) + (2.0)v_2 \\ 0 = 6 + 2.0v_2 \\ 2.0v_2 = -6 \\ v_2 = -3.0 \text{ m/s} \] Answer: The 2.0 kg piece moves left at 3.0 m/s.