Impulse-Momentum Theorem

Conceptual Definition

Impulse is the effect of a force acting over time. Think of impulse like hitting a baseball coming at you. To redirect the baseball, you have to hit it and change it's momentum. The contact might look instantantaneous, but there is still a duration of contact (even if its in miliseconds). When a force acts on an object, it changes the object's momentum. This leads to the impulse-momentum theorem:

\[ \vec{J} = \Delta \vec{p} = m \Delta \vec{v} \]

Impulse as a Time Integral

For forces that vary with time, impulse is the integral of force with respect to time:

\[ \vec{J} = \int_{t_1}^{t_2} \vec{F}(t) \, dt \]

As you can see from this formula, impulse does NOT depend on position, only the force and time.

Figure: The shaded area under the curve equals the impulse.

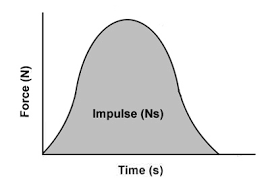
This integral represents the area under a force-time graph. For constant force, this simplifies to:

\[ \vec{J} = \vec{F} \cdot \Delta t \]

Calculus-Based Derivation

Starting from Newton’s Second Law in vector form:

\[ \vec{F}_{\text{net}} = \frac{d\vec{p}}{dt} \]

Integrate both sides over time:

\[ \int_{t_1}^{t_2} \vec{F}_{\text{net}} \, dt = \int_{t_1}^{t_2} \frac{d\vec{p}}{dt} \, dt = \vec{p}_f - \vec{p}_i = \Delta \vec{p} \]

Therefore:

\[ \vec{J} = \Delta \vec{p} \]

Units and Direction

Impulse has the same units as momentum: \(\text{kg} \cdot \text{m/s} = \text{N} \cdot \text{s}\). It is a vector quantity — its direction is the same as the direction of the net force.

Figure: Impulse vector aligns with force vector direction.

Applications

In collisions, impulse tells us how much momentum is transferred.
Airbags increase time of impact, reducing force via the same impulse.
In rockets, momentum changes due to impulse from exhaust force over time.

Example (Calculus)

A particle experiences a force described by \( F(t) = 6t \) N for \( 0 \leq t \leq 3 \) s. Find the impulse delivered.

\[ \vec{J} = \int_0^3 6t \, dt = \left[3t^2\right]_0^3 = 3(9) - 0 = 27 \, \text{N·s} \]

If the particle has mass 3 kg and was initially at rest, its final velocity is:

\[ \vec{J} = m\vec{v}_f \Rightarrow \vec{v}_f = \frac{27}{3} = 9 \, \text{m/s} \]

Summary

Impulse is the integral of force with respect to time.
Impulse changes momentum: \( \vec{J} = \Delta \vec{p} \)
Force-time graphs provide a powerful visualization tool for impulse.
Use vector and integral notation for full AP Physics C analysis.

Key Comparisons

Quantity	Definition	Units	Formula
Impulse \( \vec{J} \)	Change in momentum or area under \( \vec{F}(t) \) curve	\( \text{N·s} = \text{kg·m/s} \)	\( \vec{J} = \int \vec{F}(t)\,dt \)
Momentum \( \vec{p} \)	Product of mass and velocity	\( \text{kg·m/s} \)	\( \vec{p} = m\vec{v} \)
Force \( \vec{F} \)	Time rate of change of momentum	\( \text{N} = \text{kg·m/s}^2 \)	\( \vec{F} = \frac{d\vec{p}}{dt} \)

Impulse-Momentum Theorem Simulation

(graph rescales after impulse duration is over)

Mass (kg): 5.0

Initial Velocity (m/s): 10.0

Impulse Force (N): 0

Impulse Duration (s): 1.0

Impulse: 0 Ns

Momentum: 50.0 kg·m/s

Impulse Bar: