← Back to Concepts

Common Moments of Inertia — With Derivations

These classic shapes come up constantly in rotational motion. Below are their moments of inertia and complete calculus-based derivations using symmetry and mass density.

You do NOT have to memorize these formulas The common derivations are shown to give you an example of how to figure out the moment of inertia if asked to derive from scratch. On the test, they will give you the moment of inertia formula.

1. Solid Disk (Radius \( R \), Mass \( M \))

We slice the disk into concentric rings of radius \( r \) and thickness \( dr \), each treated like a hoop.

\( dI = r^2 \, dm \)

The area of each ring is \( dA = 2\pi r \, dr \), and mass per unit area is \( \sigma = \frac{M}{\pi R^2} \).

\( dm = \sigma \, dA = \frac{M}{\pi R^2} \cdot 2\pi r \, dr = \frac{2M}{R^2} r \, dr \)

Now integrate:

\( I = \int_0^R r^2 \cdot \frac{2M}{R^2} r \, dr = \frac{2M}{R^2} \int_0^R r^3 \, dr = \frac{2M}{R^2} \cdot \frac{R^4}{4} = \frac{1}{2}MR^2 \)

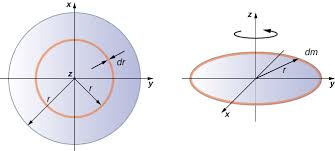
2. Thin Hoop (Radius \( R \), Mass \( M \))

For a hoop, all the mass is a fixed distance \( R \) from the center, so there's no need to integrate.

\( I = \sum m_i R^2 = M R^2 \)

3. Solid Sphere (Radius \( R \), Mass \( M \))

Consider the sphere as stacked disks of radius \( r(x) \) along the vertical axis. Each disk is at distance \( x \) from the center.

Radius at height \( x \):

\( r = \sqrt{R^2 - x^2} \)

Moment of inertia of each disk (from above): \( dI = \frac{1}{2} \, r^2 \, dm \)

Volume of each disk is \( dV = \pi r^2 dx \), and mass density is \( \rho = \frac{M}{\frac{4}{3}\pi R^3} \).

\( dm = \rho \cdot dV = \rho \pi (R^2 - x^2) dx \)

So:

\( dI = \frac{1}{2} (R^2 - x^2) \cdot \rho \pi (R^2 - x^2) dx = \frac{1}{2} \rho \pi (R^2 - x^2)^2 dx \)

Integrate from \(-R\) to \(+R\):

\( I = \int_{-R}^{R} \frac{1}{2} \rho \pi (R^2 - x^2)^2 dx \)

Use symmetry and solve the integral (or use known result):

\( I = \frac{2}{5} M R^2 \)

Other Common Moment of Inertia's

Summary Table

Solid Disk: \( \frac{1}{2}MR^2 \)
Thin Hoop: \( MR^2 \)
Solid Sphere: \( \frac{2}{5}MR^2 \)

Takeaway

The farther mass is from the axis, the larger the moment of inertia. Calculus allows us to derive these exact formulas by summing the contributions of tiny mass elements.