Momentum Conservation Principle
What is Momentum Conservation?
Momentum conservation is a fundamental principle of physics stating that in an isolated system, the total momentum remains constant if no net external force acts on it. This principle is crucial in analyzing collisions, explosions, and any interactions involving moving bodies. In simple terms, this formula is:
Even though momentum is conserved, it does not mean that kinetic energy is conserved. We will go more in depth on this later in this unit.
Why does no net external force imply conservation?
Newton's 2nd law states the rate of change of momentum equals the net external force:
This means total momentum does not change in time when no external forces act.
Vector Nature: Conservation in 1D and 2D
Since momentum is a vector, conservation applies independently to each component:
This is important for 2D collisions where vector decomposition is necessary.
Internal Forces Cancel (Newton's 3rd Law)
For any two interacting bodies inside the system (e.g. Tension force of a string in a 2-block system), internal forces come in action-reaction pairs:
For more review of Newton's 3rd Law:
Newton's 3rd LawCalculus Derivation of Momentum Conservation
The total momentum \( \vec{P} \) of a system of particles is:
Newton's second law for each particle: \( m_i \frac{d\vec{v}_i}{dt} = \vec{F}_{i,\text{external}} + \sum \vec{F}_{i,\text{internal}} \)
Summing over all particles and canceling internal forces yields:
Example: 1D Collision of Two Objects
Two objects with masses \( m_1, m_2 \) and initial velocities \( v_{1i}, v_{2i} \) collide in one dimension.
Since no external force acts, total momentum before and after satisfies:
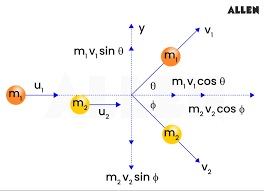
Example: 2D Collision with Momentum Conservation
In two dimensions, apply conservation separately for each component:
Common Misconceptions
- Momentum is always conserved: Only true if the system is isolated (no external forces).
- Internal forces change total momentum: Internal forces always cancel and do not change total momentum.
- Momentum is scalar: Momentum is a vector; direction matters.
Watch this video for a better understanding of momentum conservation:
Summary Table
| Concept | Explanation | Mathematical Expression |
|---|---|---|
| No Net External Force | Total momentum remains constant | \( p_i = p_f \) |
| Momentum Conservation | Initial total momentum = final total momentum | \( p_i = p_f \) |
| Vector Components | Conservation applies separately in each direction | \( p_{i,x} = p_{f,x}, \quad p_{i,y} = p_{f,y} \) |
| Internal Forces | Cancel out and don't affect total momentum | \( \sum \vec{F}_{\text{internal}} = 0 \) |
Use this principle to solve a wide variety of collision and explosion problems in AP Physics C.