← Back to Concepts

Parallel Axis Theorem

Sometimes, we know an object's moment of inertia about an axis through its center of mass (COM), but we need to calculate it about another axis, typically one that's parallel and offset by a distance \( d \). That's when the Parallel Axis Theorem becomes essential. In other words, we use the parralel axis to calculate around a different axis rather than the center of mass.

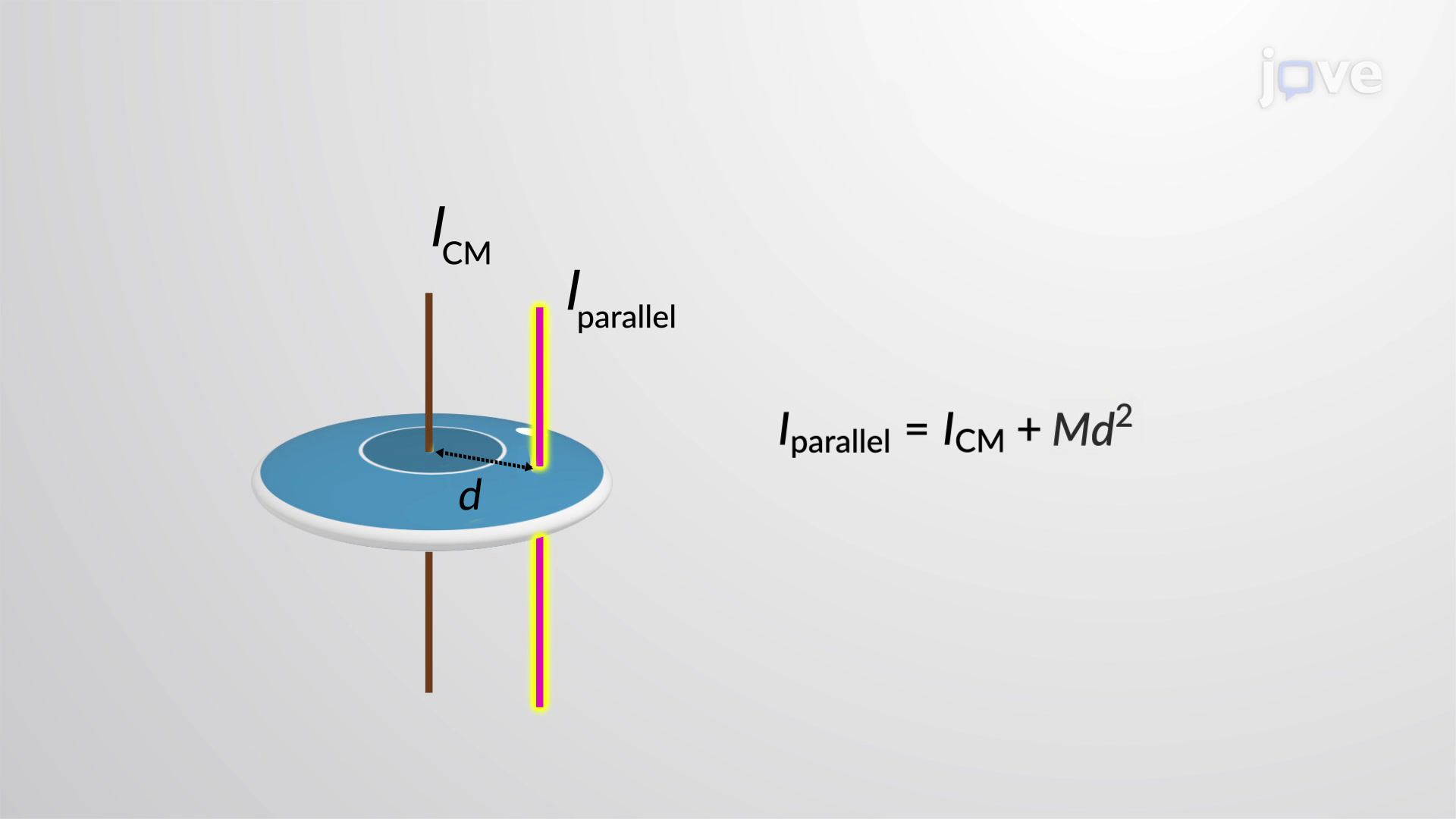
Theorem Statement

\( I = I_{\text{cm}} + Md^2 \)

Where:

\( I_{\text{cm}} \): moment of inertia through the center of mass
\( M \): total mass of the object
\( d \): perpendicular distance from COM axis to the new axis

Why It Works

The moment of inertia depends on both the amount of mass and how far that mass is from the axis. When you shift the axis, all the mass is, on average, farther away. The extra \( Md^2 \) accounts for that increased resistance to rotation.

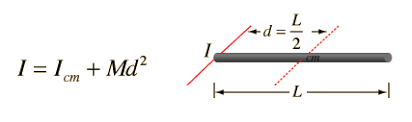
Example 1: Thin Rod, Axis at the End

For a thin rod of mass \( M \) and length \( L \), the moment of inertia about the center is:

\( I_{\text{cm}} = \frac{1}{12}ML^2 \)

To find \( I \) about one end, the axis is shifted by \( d = \frac{L}{2} \).

\( I = \frac{1}{12}ML^2 + M\left(\frac{L}{2}\right)^2 = \frac{1}{12}ML^2 + \frac{1}{4}ML^2 = \frac{1}{3}ML^2 \)

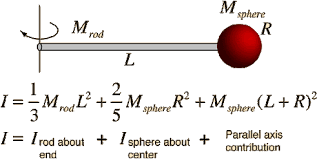
Example 2: Rod + Sphere (Composite Object)

Suppose we have a uniform rod of mass \( M_r \) and length \( L \), with a solid sphere of mass \( M_s \) and radius \( R \) attached at one end. We want the moment of inertia of the system about the opposite end of the rod.

Step 1: Rod's Contribution

The rod's own moment of inertia about the far end is:

\( I_{\text{rod}} = \frac{1}{3} M_r L^2 \)

Step 2: Sphere's Contribution

The sphere rotates about the same axis, but its center is at distance \( L + R \) from the axis.

Moment of inertia of a solid sphere about its center:

\( I_{\text{sphere, cm}} = \frac{2}{5} M_s R^2 \)

Apply parallel axis theorem to move axis to end of rod:

\( I_{\text{sphere}} = \frac{2}{5} M_s R^2 + M_s (L + R)^2 \)

Total Moment of Inertia

\( I_{\text{total}} = I_{\text{rod}} + I_{\text{sphere}} = \frac{1}{3} M_r L^2 + \left( \frac{2}{5} M_s R^2 + M_s (L + R)^2 \right) \)

Tips for Using the Theorem

Always use the object’s center-of-mass moment of inertia as your starting point.
Use this theorem when the new axis is parallel to the original one.
Great for composite objects, like pendulums or rotating beams.

Common Use Cases

Pendulums: rods or disks swinging about a pivot
Gears mounted off-center
Compound systems with multiple bodies

Summary

The Parallel Axis Theorem allows you to easily shift known moments of inertia to new axes and combine them for complex systems. It’s a key tool for analyzing rotational motion beyond idealized center-of-mass setups.

Disk + Blob Inertia Simulation

Blob Mass (kg): Distance from Center (m): 1.00 m

Moment of Inertia: —