Rolling Without Slipping

The Fundamental Condition

$$v = \omega R$$

This equation links translational and rotational motion in rolling without slipping.

When an object rolls without slipping, there's a perfect relationship between its translational velocity ($v$) and its angular velocity ($\omega$). This condition ensures that the point of contact with the surface has zero velocity relative to the surface—meaning no sliding or skidding occurs.

Physical Understanding

Rolling without slipping means the object moves forward exactly as much as it rotates. For every complete rotation ($2\pi$ radians), the object moves forward by its circumference ($2\pi R$). This creates the relationship $v = \omega R$.

Velocity at Different Points on the Wheel

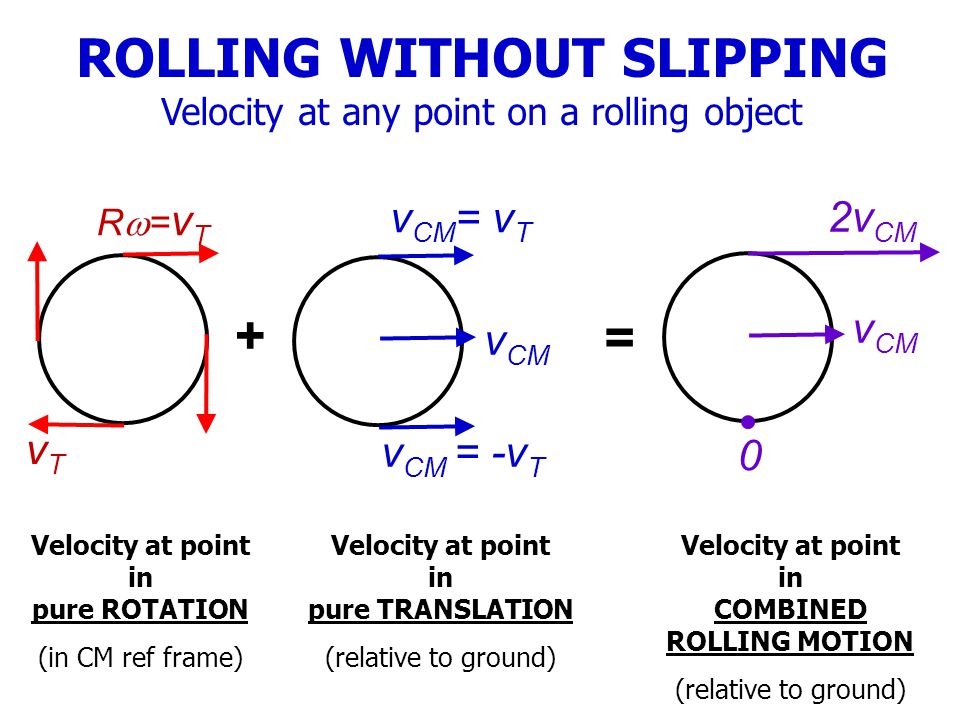
When a wheel rolls without slipping, different points on the wheel have different velocities relative to the ground. This is because each point has both translational velocity ($v$) and rotational velocity ($\omega R$).

At the Bottom (Point of Contact):

Translational velocity: $+v$ (forward)

Rotational velocity: $-v$ (backward, since the wheel is rotating)

Total velocity: $v - v = 0$

This is why the wheel doesn't slip—the point touching the ground has zero velocity relative to the ground.

At the Top:

Translational velocity: $+v$ (forward)

Rotational velocity: $+v$ (forward, since the top is moving forward)

Total velocity: $v + v = 2v$

The top of the wheel moves twice as fast as the center!

At the Center:

Translational velocity: $+v$ (forward)

Rotational velocity: $0$ (no rotational motion at the center)

Total velocity: $v + 0 = v$

The center moves at the translational velocity.

At the Sides:

Translational velocity: $+v$ (forward)

Rotational velocity: $\pm v$ (perpendicular to forward motion)

Total velocity: $\sqrt{v^2 + v^2} = v\sqrt{2}$

The sides move at $v\sqrt{2}$ at 45° angles.

Don't believe me? Watch this!

Why This Condition Matters

No Energy Loss: Rolling without slipping is energy-conserving—no kinetic energy is lost to friction
Predictable Motion: Once you know either $v$ or $\omega$, you can find the other
Real-World Applications: Wheels, gears, and many mechanical systems rely on this condition
Physics Problems: This relationship is crucial for solving rolling motion problems

Interactive Simulation: Rolling Without Slipping

Explore how translational and rotational motion are linked in rolling without slipping.

Radius (0.5-2.0 m):

Current: 1.0 m

Translational Velocity (1-5 m/s):

Current: 2.0 m/s

Mass (1-10 kg):

Current: 5.0 kg

Rolling Without Slipping Calculations:
Angular Velocity: 2.0 rad/s
Condition Check: v = ωR ✓
Total Kinetic Energy: 15.0 J
Note: The wheel rolls without slipping, maintaining v = ωR

Mathematical Derivation

Let's derive the condition $v = \omega R$ step by step:

Step 1: In rolling without slipping, the point of contact has zero velocity relative to the surface.

Step 2: The velocity of any point on the wheel is the sum of translational velocity ($v$) and rotational velocity ($\omega R$).

Step 3: At the point of contact: $v_{\text{contact}} = v - \omega R = 0$

Step 4: Therefore: $v = \omega R$

Energy in Rolling Motion

When an object rolls without slipping, it has both translational and rotational kinetic energy:

$$K_{\text{total}} = K_{\text{trans}} + K_{\text{rot}} = \frac{1}{2}mv^2 + \frac{1}{2}I\omega^2$$

Using the rolling condition $v = \omega R$ and moment of inertia $I = k m R^2$ (where $k$ depends on the shape), we can express the total kinetic energy in terms of just the translational velocity:

$$K_{\text{total}} = \frac{1}{2}mv^2 + \frac{1}{2}(k m R^2)\left(\frac{v}{R}\right)^2 = \frac{1}{2}mv^2(1 + k)$$

Common Values of k (Shape Factor)

Shape	Moment of Inertia	k Value	Total Energy Factor
Solid Sphere	$I = \frac{2}{5}mR^2$	0.4	1.4
Solid Cylinder	$I = \frac{1}{2}mR^2$	0.5	1.5
Hollow Cylinder	$I = mR^2$	1.0	2.0
Solid Disk	$I = \frac{1}{2}mR^2$	0.5	1.5

Example 1: Car Tire Rolling

A car tire with radius $0.3\,\text{m}$ is rolling at $20\,\text{m/s}$. What is its angular velocity?

Solution:

Using $v = \omega R$:

$\omega = \frac{v}{R} = \frac{20}{0.3} = 66.7\,\text{rad/s}$

This is about 637 RPM (revolutions per minute).

Example 2: Rolling Down an Incline

A solid sphere of mass $2\,\text{kg}$ and radius $0.1\,\text{m}$ rolls down a hill. If it reaches a speed of $5\,\text{m/s}$, what is its total kinetic energy?

Solution:

For a solid sphere, $k = 0.4$

$K_{\text{total}} = \frac{1}{2}mv^2(1 + k) = \frac{1}{2} \times 2 \times 5^2 \times 1.4 = 35\,\text{J}$

Note: Only 71% of the energy is translational, 29% is rotational.

Example 3: Comparing Rolling Objects

Two objects with the same mass and radius roll down the same incline: a solid sphere and a hollow cylinder. Which reaches the bottom first?

Solution:

Solid sphere: $k = 0.4$, so more energy goes to translation

Hollow cylinder: $k = 1.0$, so more energy goes to rotation

Answer: The solid sphere reaches the bottom first because it has a lower moment of inertia and thus more translational kinetic energy.

Real-World Applications

Automotive Engineering: Tire design and vehicle dynamics rely on rolling without slipping
Sports Equipment: Balls, wheels, and other rolling objects in sports
Industrial Machinery: Conveyors, rollers, and mechanical systems
Transportation: Trains, bicycles, and other wheeled vehicles
Physics Experiments: Rolling motion is used to study energy conservation and rotational dynamics

Common Misconceptions

Myth: "Rolling objects only have translational energy"
Reality: Rolling objects have both translational and rotational kinetic energy
Myth: "All rolling objects behave the same way"
Reality: Shape affects the distribution of energy between translation and rotation
Myth: "Rolling friction is the same as sliding friction"
Reality: Rolling friction is typically much smaller than sliding friction

Advanced Concepts

Rolling with Slipping

When $v \neq \omega R$, the object is either skidding or spinning in place. This creates kinetic friction that acts to restore the rolling condition.

Rolling Resistance

Even in rolling without slipping, there's still some energy loss due to deformation of the rolling object and the surface. This is called rolling resistance.

Summary / Takeaways

The condition $v = \omega R$ defines rolling without slipping
This condition ensures no energy loss to sliding friction
Rolling objects have both translational and rotational kinetic energy
The shape of the object affects how energy is distributed
Understanding rolling motion is crucial for many engineering applications
The relationship between $v$ and $\omega$ is fundamental to rotational dynamics