Solving Collision Problems
Solving collision problems involves applying the principle of momentum conservation—and sometimes kinetic energy conservation—depending on the type of collision.
General Strategy
- Identify the type of collision: elastic, inelastic, or perfectly inelastic
- Apply conservation of momentum: \( m_1v_{1,i} + m_2v_{2,i} = m_1v_{1,f} + m_2v_{2,f} \)
- Use kinetic energy conservation only if the collision is elastic
- Solve algebraically or plug in values if known
Example 1: Perfectly Inelastic Collision
Problem: A 1.5 kg cart moving at 2 m/s collides with a 0.5 kg cart at rest. They stick together. What is their final velocity?
Perfectly inelastic – objects stick together, momentum conserved, KE not.
Answer: They move together at 1.5 m/s.
Example 2: Elastic Collision (Equal Masses)
Problem: A 0.6 kg ball moving at 3 m/s hits a stationary 0.6 kg ball. What are the final velocities?
In 1D, identical masses simply swap velocities in an elastic collision.
Answer: First ball stops; second ball moves at 3 m/s.
Example 3: Elastic Collision (Unequal Masses)
Problem: A 2 kg cart moving at 4 m/s hits a 1 kg stationary cart. What are the final velocities if the collision is elastic?
Answer: Cart 1: 1.33 m/s, Cart 2: 5.33 m/s
Example 4: Inelastic but Not Perfectly
Problem: A 3 kg object moving at 6 m/s hits a 2 kg object moving at 2 m/s. After colliding, they bounce off with different velocities. Final velocity of object 2 is 4 m/s. What is object 1’s final velocity?
Answer: Object 1’s final velocity is approximately 4.67 m/s
Example 5: Kinetic Energy Loss
Problem: A 2 kg object moving at 3 m/s collides with a 2 kg object at rest. They stick together. How much kinetic energy is lost?
Answer: 4.5 J of kinetic energy is lost.
Example 6: Percent KE Loss
Problem: In the previous example, what percent of the initial kinetic energy is lost?
Answer: 50% of the initial kinetic energy was lost in the collision.
Example 7: Ballistic Pendulum
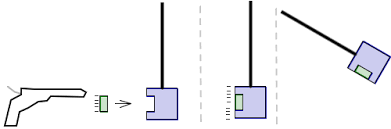
Problem: A 0.02 kg bullet traveling at 300 m/s embeds into a 1 kg wooden block hanging from a string. How high does the block-bullet system rise after the collision?
Answer: The system rises approximately 1.76 meters.
Key Tips for Solving
- Always write the momentum conservation equation first
- If elastic, write the kinetic energy equation or use special formulas
- For perfectly inelastic, use the combined mass final velocity formula
- Draw before/after diagrams to visualize motion
Summary
Collision problems are highly solvable with momentum conservation. The collision type tells you whether you can also use kinetic energy conservation. Practice identifying types and setting up equations systematically!