Torque Definition

Torque is the rotational equivalent of force. It describes how a force causes an object to rotate about a specific axis or pivot point. The effectiveness of a force in producing rotation depends on the force's magnitude, direction, and where it is applied relative to the axis.

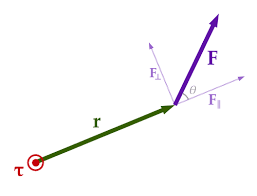
Where:

• $\tau$ is torque (in N·m)
• $r$ is the distance from the axis of rotation to the point where the force is applied
• $F$ is the magnitude of the force
• $\theta$ is the angle between the position vector and the force vector

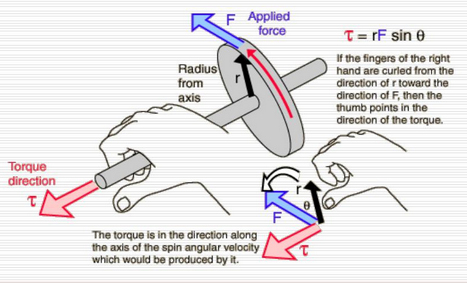
Cross Product Form

Torque is more formally defined as the cross product of the position vector $\vec{r}$ and the force vector $\vec{F}$:

The magnitude of the torque is:

The direction of $\vec{\tau}$ is perpendicular to the plane formed by $\vec{r}$ and $\vec{F}$, determined using the right-hand rule.

Lever Arm Form

The lever arm is the perpendicular distance from the axis of rotation to the line of action of the force. Torque can also be calculated using:

This form is especially useful when the perpendicular distance is known or easier to find than the angle.

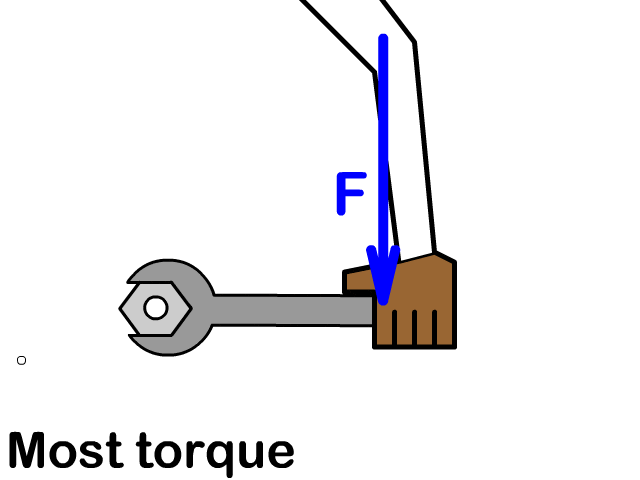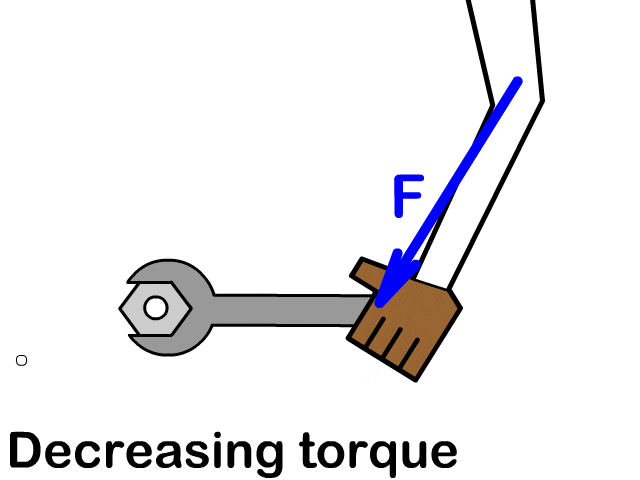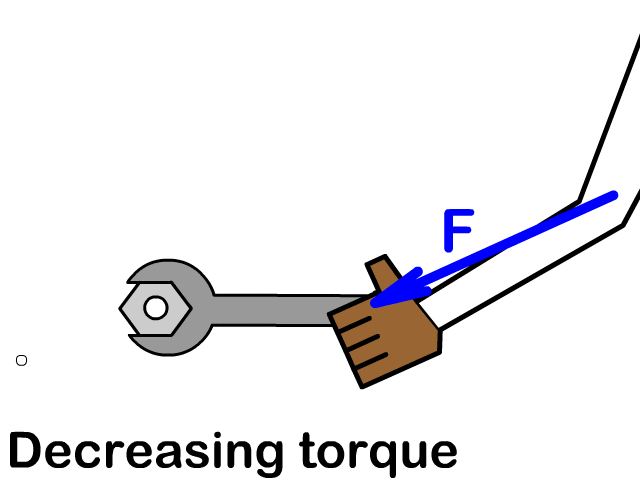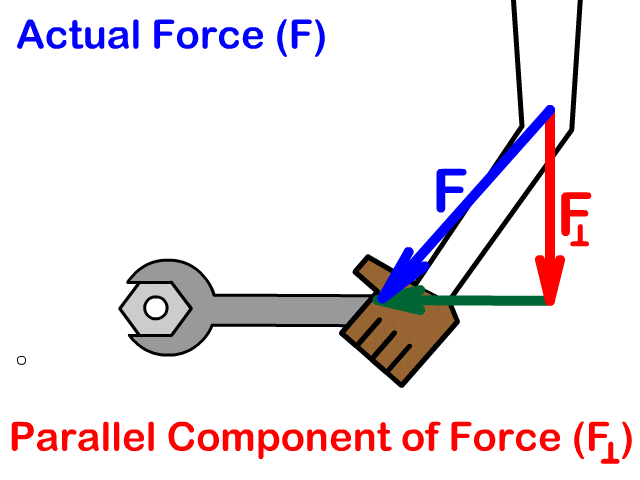
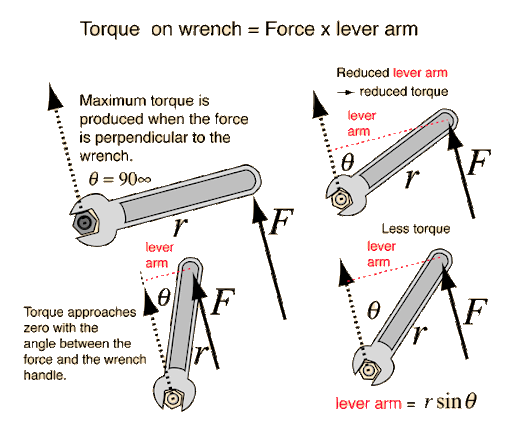
Example 1: Force Perpendicular to Lever Arm

Example 2: Force at an Angle

Example 3: Using Lever Arm

VERY HELPFUL VIDEO:

Summary and Takeaways

• Torque quantifies the ability of a force to cause rotation around an axis.
• It depends on the magnitude of the force, the distance from the axis, and the angle of application.
• The cross product $\vec{\tau} = \vec{r} \times \vec{F}$ provides the direction and magnitude of torque in vector form.
• Maximum torque occurs when the force is applied perpendicular to the position vector ($\theta = 90^\circ$).
• The lever arm method simplifies torque calculations when the perpendicular distance is known: $\tau = r_\perp \cdot F$.
• Use the right-hand rule to determine the direction of torque vectors.