Solenoid Basics
A solenoid is a coil of wire wound in a helical pattern that creates a uniform magnetic field when current flows through it. Solenoids are fundamental components in electromagnetism and have numerous practical applications.
What is a Solenoid?
🧲 Solenoid Definition
A solenoid is a long coil of wire with many turns that produces a nearly uniform magnetic field inside when current flows through it.
The magnetic field inside a solenoid is approximately uniform and parallel to the axis of the coil.
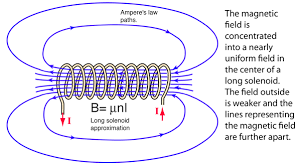
Solenoid Diagrams
In diagrams, solenoids are often represented using "×" (cross) to indicate current or field going into the page, and "●" (dot) to indicate current or field coming out of the page. This notation helps visualize the three-dimensional direction of current or magnetic field lines in two-dimensional drawings.


Magnetic Field Inside a Solenoid
⚡ Field Calculation Using Ampère's Law
The magnetic field inside a long solenoid can be calculated using Ampère's Law:
Where:
- \( B \) is the magnetic field strength
- \( \mu_0 \) is the permeability of free space (4π × 10⁻⁷ T⋅m/A)
- \( n \) is the number of turns per unit length
- \( I \) is the current through the solenoid

Derivation Using Ampère's Law
To derive this formula using Ampère's Law:
- Choose Amperian Loop: Use a rectangular loop with one side inside the solenoid
- Apply Ampère's Law: \( \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} \)
- Calculate Enclosed Current: \( I_{enc} = nLI \) where \( L \) is the length of the loop
- Evaluate the Integral: \( BL = \mu_0 nLI \)
- Solve for B: \( B = \mu_0 nI \)
Key Properties of Solenoids
🔬 Important Characteristics
- Uniform Field: The magnetic field is nearly uniform inside a long solenoid
- Field Direction: Use the right-hand rule to determine field direction
- Field Strength: Proportional to current and turns per unit length
- End Effects: Field is weaker near the ends of the solenoid
- External Field: Much weaker outside the solenoid
Right-Hand Rule for Solenoids
- Grasp the Solenoid: Wrap your right hand around the solenoid
- Finger Direction: Point your fingers in the direction of current flow
- Thumb Direction: Your thumb points in the direction of the magnetic field inside
- Field Lines: The field lines run parallel to the axis inside the solenoid
Example: Solenoid Field Calculation
Problem: A solenoid has 1000 turns per meter and carries a current of 2.0 A. Calculate the magnetic field inside the solenoid.
Step 1: Identify Given Values
- \( n = 1000 \) turns/m
- \( I = 2.0 \) A
- \( \mu_0 = 4\pi \times 10^{-7} \) T⋅m/A
Step 2: Apply the Formula
Step 3: Calculate
Step 4: Direction
Use the right-hand rule to determine the field direction along the solenoid axis.
Magnetic Flux in Solenoids
🔗 Connection to Magnetic Flux
The magnetic flux through a solenoid is related to the field strength:
Where \( A \) is the cross-sectional area of the solenoid.
This connects to the fundamental concept of magnetic flux and how it relates to the magnetic field.
Flux Linkage
- Total Flux: \( \Phi_{total} = N\Phi_B = N\mu_0 nIA \)
Factors Affecting Solenoid Performance
Length and Diameter
- Long Solenoids: More uniform field, better approximation
- Short Solenoids: Non-uniform field, end effects important
- Diameter: Larger diameter means more turns needed for same field
Core Material Effects
- Air Core: Uses the formula \( B = \mu_0 nI \)
- Iron Core: Field enhanced by factor of relative permeability \( \mu_r \)
- Ferromagnetic Core: Can increase field by 1000+ times
- Superconducting Core: Can create extremely strong fields
How Core Material Affects the Solenoid
The material inside the solenoid (the core) significantly affects its magnetic field strength:
- Air Core: No enhancement, field follows \( B = \mu_0 nI \)
- Iron Core: Field becomes \( B = \mu_r \mu_0 nI \) where \( \mu_r \) is the relative permeability
- Ferromagnetic Materials: Can have \( \mu_r \) values of 1000-100,000, dramatically increasing field strength
- Core Saturation: At high fields, ferromagnetic materials saturate and stop enhancing the field
- Hysteresis: Ferromagnetic cores have memory effects that can affect performance
Comparison with Other Magnetic Field Sources
vs. Single Current Loop
- Solenoid: Uniform field, many turns
- Single Loop: Non-uniform field, one turn
- Field Strength: Solenoid field is \( n \) times stronger per unit current
vs. Straight Wire
- Solenoid: Field inside is uniform and strong
- Straight Wire: Field decreases with distance, circular pattern
- Applications: Solenoids used where uniform field is needed
Quick Quiz: Solenoid Basics
1. What law is used to calculate the magnetic field inside a solenoid?
2. What is the formula for magnetic field inside a solenoid?
3. How do you determine the direction of the magnetic field in a solenoid?
Key Takeaways
- Uniform Field: Solenoids create nearly uniform magnetic fields inside
- Ampère's Law: Used to derive the field formula \( B = \mu_0 nI \)
- Right-Hand Rule: Determines field direction based on current flow
- Flux Connection: Links to magnetic flux concepts
- Practical Device: Foundation for many electromagnetic applications