Toroidal Coils
A toroidal coil (or toroid) is a coil of wire wound in a donut-shaped form that creates a magnetic field confined primarily within the torus. Toroidal coils are important in electromagnetism because they provide excellent magnetic field confinement and are used in various applications.
What is a Toroidal Coil?
🧲 Toroidal Coil Definition
A toroidal coil is a coil of wire wound in a circular or donut shape that creates a magnetic field primarily confined within the torus.
The magnetic field lines form closed loops within the toroid, with minimal external field leakage.

Toroid Diagram
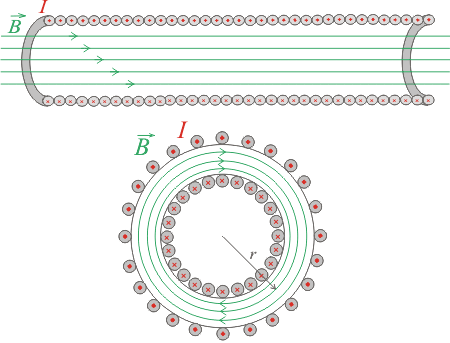
Magnetic Field Inside a Toroid
⚡ Field Calculation Using Ampère's Law
The magnetic field inside a toroid can be calculated using Ampère's Law:
Where:
- \( B \) is the magnetic field strength
- \( \mu_0 \) is the permeability of free space (4π × 10⁻⁷ T⋅m/A)
- \( N \) is the total number of turns
- \( I \) is the current through the coil
- \( r \) is the distance from the center of the toroid
Derivation Using Ampère's Law
To derive this formula using Ampère's Law:
- Choose Amperian Loop: Use a circular path inside the toroid
- Apply Ampère's Law: \( \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} \)
- Calculate Enclosed Current: \( I_{enc} = NI \) where \( N \) is the total number of turns
- Evaluate the Integral: \( B(2\pi r) = \mu_0 NI \)
- Solve for B: \( B = \frac{\mu_0 NI}{2\pi r} \)
Watch this For Better Understanding:
Key Properties of Toroidal Coils
🔬 Important Characteristics
- Field Confinement: Magnetic field is confined within the toroid
- Minimal Leakage: Very little external magnetic field
- Field Variation: Field strength varies with radius inside the toroid
- Field Confinement: Excellent for applications requiring confined fields
- Efficient Design: More efficient than solenoids for some applications
Field Distribution
- Inside the Toroid: Field is strongest near the inner radius
- Field Direction: Use the right-hand rule to determine direction
- Outside the Toroid: Field is approximately zero
- Uniformity: Field is more uniform than in a solenoid
Example: Toroidal Coil Field Calculation
Problem: A toroidal coil has 1000 turns and carries a current of 2.0 A. The inner radius is 5.0 cm and the outer radius is 7.0 cm. Calculate the magnetic field at a radius of 6.0 cm.
Step 1: Identify Given Values
- \( N = 1000 \) turns
- \( I = 2.0 \) A
- \( r = 6.0 \) cm = 0.060 m
- \( \mu_0 = 4\pi \times 10^{-7} \) T⋅m/A
Step 2: Apply the Formula
Step 3: Calculate
Step 4: Direction
Use the right-hand rule to determine the field direction around the toroid.
Comparison with Solenoids
Advantages of Toroidal Coils
- Field Confinement: No external field leakage
- Efficiency: More efficient use of magnetic material
- Efficiency: Higher efficiency per unit volume
- Interference: Minimal interference with nearby components
- Applications: Better for applications requiring confined fields
Disadvantages of Toroidal Coils
- Manufacturing: More difficult to wind than solenoids
- Cost: Generally more expensive to manufacture
- Size Limitations: Limited by toroid size
- Accessibility: Harder to access the center region
Applications of Toroidal Coils
⚡ Practical Applications
Toroidal coils are used in various applications:
- Transformers: Power transformers and signal transformers
- Current Sensors: Current transformers for measurement
- Magnetic Confinement: Plasma confinement in fusion research
- Magnetic Confinement: Plasma confinement in fusion research
Transformer Applications
- Power Transformers: Efficient energy transfer with minimal losses
- Signal Transformers: Audio and communication transformers
- Isolation Transformers: Electrical isolation between circuits
- Impedance Matching: Match impedance between circuits
Current Sensing
- Current Transformers: Measure high currents safely
- Ground Fault Detection: Detect current imbalances
- Power Monitoring: Monitor power consumption
- Protection Systems: Overcurrent protection
Magnetic Flux in Toroidal Coils
Flux Calculation
The magnetic flux through a toroidal coil is:
Where \( h \) is the height of the toroid and \( r_1, r_2 \) are the inner and outer radii.
Design Considerations
Geometric Factors
- Aspect Ratio: Ratio of outer to inner radius affects field uniformity
- Winding Density: Number of turns per unit length
- Core Material: Ferromagnetic cores increase inductance
- Wire Gauge: Determines current-carrying capacity
Electrical Factors
- Resistance: \( R = \rho \frac{l}{A} \) where \( l \) is wire length
- Power Loss: \( P = I^2R \) dissipated in the wire
- Quality Factor: \( Q = \frac{\omega L}{R} \) for AC applications
- Resonance: Natural frequency \( f = \frac{1}{2\pi\sqrt{LC}} \)
Comparison with Other Magnetic Field Sources
vs. Solenoids
- Field Confinement: Toroids have better field confinement
- Efficiency: Toroids are more efficient for energy storage
- Manufacturing: Solenoids are easier to manufacture
- Applications: Each is better suited for different applications
vs. Single Current Loops
- Field Strength: Toroids have much stronger fields
- Field Uniformity: Toroids have more uniform fields
- Field Confinement: Toroids have much better field confinement
- Applications: Toroids are better for applications requiring confined fields
Quick Quiz: Toroidal Coils
1. What is the main advantage of toroidal coils over solenoids?
2. What law is used to calculate the magnetic field in a toroid?
3. What is the formula for magnetic field inside a toroid?
Key Takeaways
- Field Confinement: Toroidal coils provide excellent magnetic field confinement
- Ampère's Law: Used to derive the field formula \( B = \frac{\mu_0 NI}{2\pi r} \)
- Energy Storage: Excellent for inductive energy storage applications
- Transformer Applications: Widely used in power and signal transformers
- Efficiency: More efficient than solenoids for many applications