Circular Motion
Circular motion occurs when an object moves along a circular path with a constant speed. Even if the speed is constant, the object is accelerating due to the continuous change in direction of velocity. This acceleration is called centripetal acceleration.
Key Concepts
- Centripetal force is the net force that causes an object to move in a circle.
- This force always points toward the center of the circle.
- There is no outward "centrifugal" force acting on the object (that's a fictitious force).
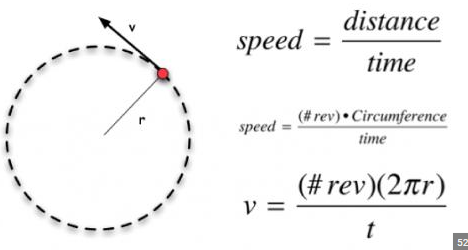
Centripetal acceleration: ac = v² / r = rω² | where ac is the centripital (radial) acceleration, v is the tangental velocity, and ω is the angular velocity (ω=v/r)
Centripetal force: Fc = mv² / r
Period of motion (amount of time to complete one revolution): T = 2πr / v
Common Units
| Quantity | Symbol | Unit |
|---|---|---|
| Velocity | v | m/s |
| Radius | r | m |
| Mass | m | kg |
| Acceleration | ac | m/s² |
| Force | Fc | N |
Example Problems
Question: A 2 kg object moves in a circle of radius 4 m at a speed of 6 m/s. What is the centripetal force acting on it?
Solution:
Use Fc = mv² / r:
Fc = (2)(6²)/4 = 72/4 = 18 N
Question: A car is driving on a circular race track and is driving at a velocity of 30 m/s. If the coefficient of static friction is 0.7, what is the minimum radius the circular track can have?
Solution:

R = 30²/(9.8*0.7) = 131.2 m
Question: A ball is attached to a string that is at an angle of θ degrees. If the ball weighs 10 kg and the radius of the circle that its traveling on is 4m at a velocity of 5m/s, find the force of tension in the string and the angle.
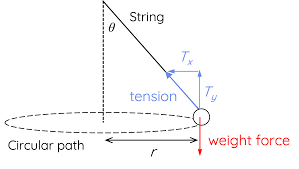
Solution:
1. Ty = Tcosθ=mg = 10*9.8 = 98 [N]
2. Tx = Tsinθ = mv² / r = 10*5² / 4 = 62.5 [N]
3. √(Tx² + Ty²) = T
4. T = √(98)²+(62.5)² = 116.23
5. θ = tan-1(Tx/Ty) = 32.5 degrees
Banked Curves
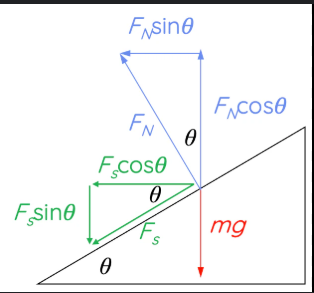
When a car turns on a flat road, the frictional force between the tires and the road provides the necessary centripetal force to keep the car moving in a circle. However, if the road is banked (tilted at an angle), the situation becomes more interesting.
Why Banked Curves Help
On a banked curve, the normal force — which is perpendicular to the surface of the road — has a component that can help supply the centripetal force needed for circular motion. This reduces the reliance on friction alone.

If the banking angle is ideal for a certain speed, a car can round the curve with no friction at all, relying solely on the horizontal component of the normal force to provide the necessary centripetal force.
tan(θ) = v² / (r·g)
where:
- θ = banking angle
- v = speed of the object
- r = radius of the curve
- g = acceleration due to gravity
Forces at Work
- Normal Force (N): Acts perpendicular to the banked surface; its horizontal component provides part (or all) of the centripetal force.
- Frictional Force (f): Acts parallel to the surface; it can help or oppose the centripetal direction depending on speed.
- Centripetal Force (Fc): Required to keep the car in circular motion; directed toward the center of the curve.
Important to Note
- If the centripital force is removed, the object will continue in a path that is tangent to the circle.
- In other words it won't keep going in a circle and exit going in the direction that was tangent to the circle.