Conservative vs Non-Conservative Forces
Forces can be classified as conservative or non-conservative based on how they affect the mechanical energy of a system.
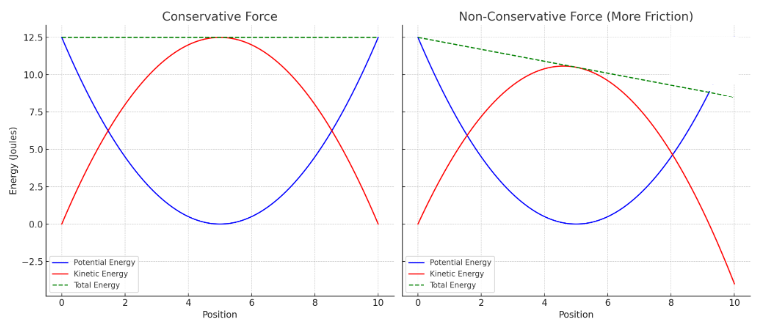
Conservative Forces
Conservative forces store energy that can be fully recovered. The work done by these forces is path-independent (only the displacement matters, not distance) and depends only on initial and final positions.
- Examples: gravity, spring force, electrostatic force
- Work done around a closed loop is zero
\[
W_{\text{closed}} = 0 \quad \text{(for conservative forces)}
\]
Non-Conservative Forces
Non-conservative forces cause energy dissipation (e.g., as heat or sound). Work done by them depends on the path taken.
- Examples: friction, air resistance, applied force
- Mechanical energy is not conserved in their presence
\[
\Delta E_{\text{mechanical}} = W_{\text{non-conservative}}
\]
Comparison Table
- Conservative: Converts between KE and PE; total ME constant
- Non-Conservative: Reduces total ME; energy lost as heat, etc.
Example
A pendulum swinging without air resistance is under conservative forces. If air resistance is introduced, the system becomes non-conservative, and the pendulum eventually stops.
Graphical Representation