General Solution to Simple Harmonic Motion
Once you understand that SHM is governed by a restoring force, the next step is learning how to describe the motion mathematically. This is where calculus and trigonometry meet physics!
1. Position Function
The motion of an object in SHM is described by a cosine (or sine) function. The most general solution is:
Where:
- \( x(t) \): Position at time \( t \)
- \( A \): Amplitude (maximum displacement)
- \( \omega \): Angular frequency \( = \sqrt{\frac{k}{m}} \) for a spring, \( \sqrt{\frac{g}{L}} \) for a pendulum
- \( \phi \): Phase constant (depends on where the object starts)
2. Velocity Function
Velocity is the derivative of position with respect to time:
Velocity is zero at maximum displacement (where the object turns around) and maximum at the equilibrium point.
3. Acceleration Function
Acceleration is the derivative of velocity (or second derivative of position):
Notice how acceleration is proportional to position but in the opposite direction — that's the hallmark of SHM.
4. Physical Meaning of Constants
- Amplitude \( A \): Maximum distance from equilibrium
- Angular Frequency \( \omega \): How fast the object oscillates (in radians/second)
- Phase Constant \( \phi \): Shifts the graph to match starting position and velocity
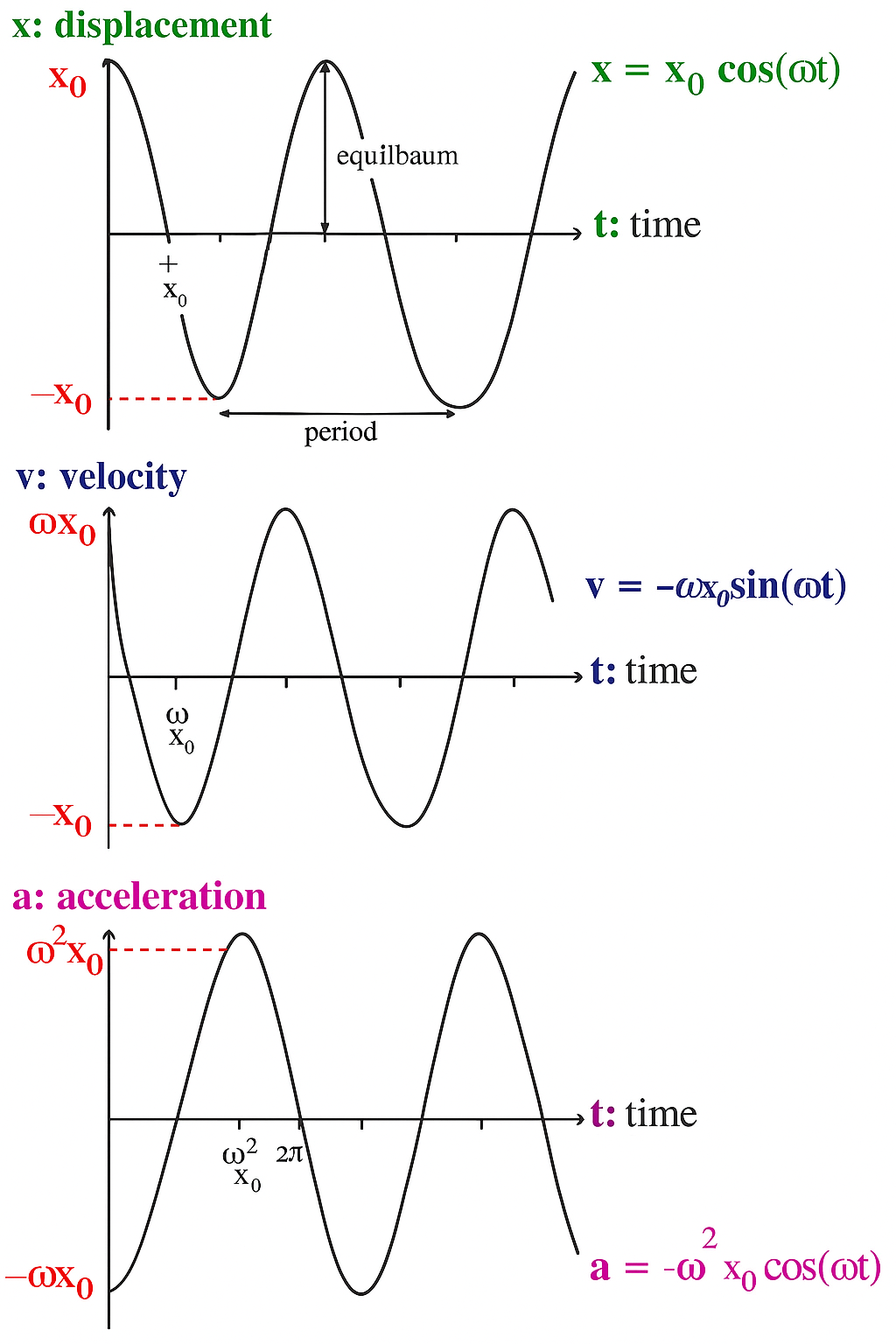
5. Graphical Understanding
- \( x(t) \): Peaks and troughs = maximum displacement
- \( v(t) \): Crosses zero at max displacement, peaks at equilibrium
- \( a(t) \): Always opposite in sign to position
6. Why This Matters
These equations let you predict where the object is, how fast it’s moving, and how it’s accelerating at any moment — all using a single formula. This is especially powerful when solving for energy, timing, or motion comparisons in SHM problems.