Gravitational Potential Energy

1. For Point Masses

The gravitational potential energy U between two point masses \( m_1 \) and \( m_2 \) separated by a distance \( r \) is:

\( U = -G \frac{m_1 m_2}{r} \)

Here, \( G \) is the universal gravitational constant.

2. Why is Gravitational Potential Energy Greatest at \( r \to \infty \)?

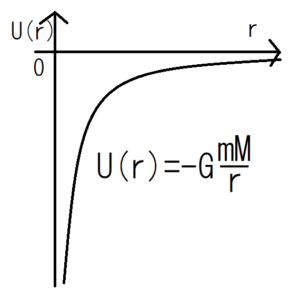
The formula shows \( U = -G \frac{m_1 m_2}{r} \), which means the potential energy is negative and depends inversely on distance \( r \). As \( r \to \infty \), the denominator becomes very large, so \( U \to 0 \).

Although zero might seem "small," remember gravitational potential energy is defined relative to zero at infinite separation. Since \( U \) is negative for any finite \( r \), it means the system is bound. When \( r \to \infty \), the negative potential energy approaches zero from below, which is the highest possible gravitational potential energy value the system can have.

In simpler terms, gravitational potential energy is always negative due to the attractive nature of gravity. The zero reference point is set at infinite separation, meaning:

At finite distances, \( U < 0 \) — the objects are bound together.
At infinite distance, \( U = 0 \) — the objects are free, unbound, and gravitational interaction is negligible.

3. Using Conservation of Energy to Show Kinetic Energy Increases as Distance Decreases

Consider an object of mass \( m \) influenced by a mass \( M \), and two distances \( r_1 \) and \( r_2 \) such that \( r_2 < r_1 \). The gravitational potential energies are:

\( U_1 = -G \frac{M m}{r_1} \quad\text{and}\quad U_2 = -G \frac{M m}{r_2} \)

Since \( r_2 < r_1 \), it follows that \( |U_2| > |U_1| \) (more negative), so:

\( U_2 < U_1 \)

Now, assume the object starts at rest infinitely far away where \( U_\infty = 0 \) and kinetic energy \( K_\infty = 0 \), and falls freely inward:

At distance \( r_1 \), kinetic energy \( K_1 = -U_1 = G \frac{M m}{r_1} \)
At closer distance \( r_2 \), kinetic energy \( K_2 = -U_2 = G \frac{M m}{r_2} \)

Because \( r_2 < r_1 \), this means:

\( K_2 > K_1 \)

Thus, the kinetic energy increases as the object gets closer to the mass, converting more gravitational potential energy into kinetic energy.

Comparison with Object Starting at Finite Distance

If the object started at rest at \( r_1 \), its kinetic energy would be zero at that position. But if it fell all the way from infinity to \( r_1 \), it would have kinetic energy \( K_1 \) as shown above.

This means the object falling from infinity to \( r_1 \) has more kinetic energy than an object simply placed at \( r_1 \) without velocity.

4. Relationship to Escape Speed

Escape speed \( v_{esc} \) is the minimum speed an object needs to escape the gravitational field of a body without further propulsion. It can be derived using energy conservation:

Derivation of Escape Speed

At the surface of a planet of mass \( M \) and radius \( r \), an object of mass \( m \) has:

Kinetic Energy (KE): \( \frac{1}{2} m v_{esc}^2 \)
Gravitational Potential Energy (PE): \( U = - G \frac{M m}{r} \)

To just escape, the total energy at infinity should be zero (no kinetic or potential energy):

\[ \text{Total Energy at surface} = \text{Total Energy at infinity} = 0 \] \[ \frac{1}{2} m v_{esc}^2 - G \frac{M m}{r} = 0 \]

Rearranging to solve for \( v_{esc} \):

\[ \frac{1}{2} m v_{esc}^2 = G \frac{M m}{r} \] \[ v_{esc}^2 = \frac{2GM}{r} \] \[ \boxed{ v_{esc} = \sqrt{\frac{2GM}{r}} } \]

5. Comparison to Spring and Near-Earth Potential Energy

Near the Earth's surface, the gravitational potential energy simplifies to:

\( U = mgh \)

where:

m: mass of the object
g: acceleration due to gravity (~9.8 m/s²)
h: height above the reference point

Summary:

Gravitational potential energy for point masses decreases with distance and is negative, reflecting the bound nature of gravitational attraction. The escape speed formula arises from setting kinetic energy equal to the magnitude of gravitational potential energy, and near the Earth's surface, gravitational potential energy approximates to \( mgh \), similar to the potential energy of a spring.