Hooke's Law in Dynamics

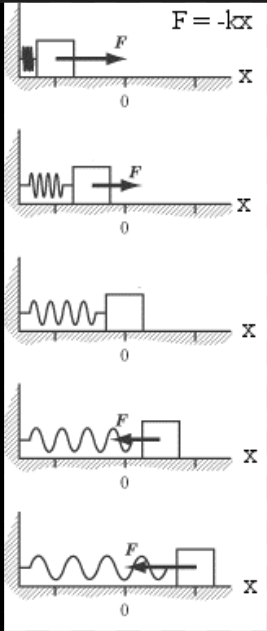
Introduction to Hooke's Law

Hooke's Law describes how elastic materials behave when stretched or compressed. Formulated by Robert Hooke, it states that the restoring force exerted by a spring is proportional to the displacement from equilibrium.

F = -kx

• F: Restoring force (N)
• k: Spring constant (N/m)
• x: Displacement from equilibrium (m)
• Negative sign shows the force is opposite to displacement

Physical Meaning and Implications

A stretched or compressed spring stores potential energy and exerts a force that returns it to its original shape. The spring constant determines how stiff the spring is. The law holds true only within the material's elastic limit.

Applications of Hooke's Law in Dynamics

In dynamics, Hooke's Law models forces affecting motion, such as a block compressing a spring. The spring slows the object, stops it, and then pushes it back. Newton's second law is used alongside Hooke's Law to solve these problems.

Key Points to Remember

• Applies within the elastic limit of a material
• Force is opposite to displacement
• k indicates stiffness
• Essential for oscillations, vibrations, and spring-based technology

Springs in Series and Parallel

When multiple springs are combined, their overall stiffness (spring constant) changes depending on how they are connected:

• Series: Springs are connected end-to-end. The equivalent spring constant is:
  \[ \frac{1}{k_{eq}} = \frac{1}{k_1} + \frac{1}{k_2} \]

  Series springs are softer than either spring alone.

• Parallel: Springs are connected side-by-side. The equivalent spring constant is:
  \[ k_{eq} = k_1 + k_2 \]

  Parallel springs are stiffer than either spring alone.

Example Questions and Solutions

Example 1: Finding Spring Force

Question: A spring is stretched by 0.2 m. If k = 300 N/m, what is the force?

Solution: F = -kx = -(300)(0.2) = -60 N

Example 2: Finding Spring Constant

Question: A force of 10 N stretches a spring 5 cm. Find k.

Solution: Convert 5 cm to meters: 0.05 m. k = F / x = 10 / 0.05 = 200 N/m

Example 3: Block Sliding into a Spring

Question: A 1.5 kg block moving at 2 m/s compresses a spring (k = 500 N/m). How far?

Solution:

• Energy: ½mv² = ½kx² → mv² = kx²
• (1.5)(2²) = 500x² → 6 = 500x²
• x² = 0.012 → x = √0.012 ≈ 0.11 m

Example 4: Direction of Force

Question: A spring is compressed 0.1 m, and k = 150 N/m. Find the force direction and magnitude.

Solution: F = -kx = -150 × 0.1 = -15 N

Visual Explanation