← Back to Concepts

Newton’s Law of Universal Gravitation

Before, in dynamics, we only used the formula F = mg. This formula can only be used when we are in the Earth's atmosphere. But what do we use when we exit our atmosphere?

Newton, along with his other formulas, gave a formula that would be known as the universal gravitational force:

\[ F_g = G \frac{m_1 m_2}{r^2} \]

\( F \): gravitational force between two masses
\( G = 6.674 \times 10^{-11} \, \text{N} \cdot \text{m}^2/\text{kg}^2 \): universal gravitational constant (always this value)
\( m_1, m_2 \): the masses of the objects
\( r \): the distance between the centers of mass of the objects

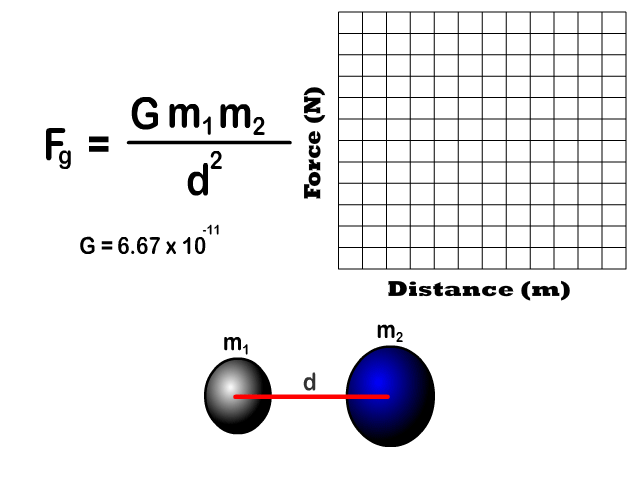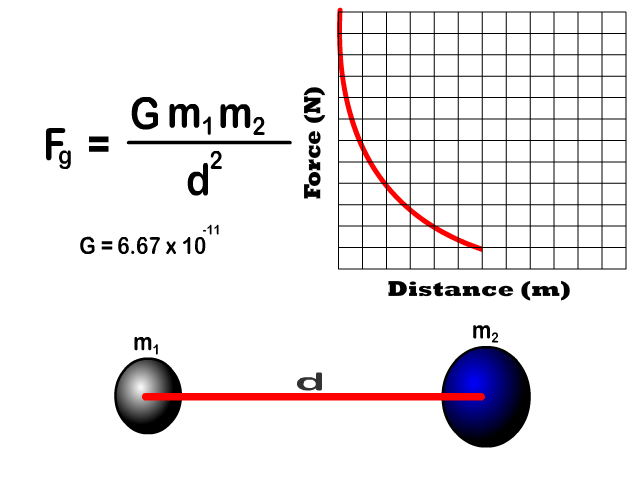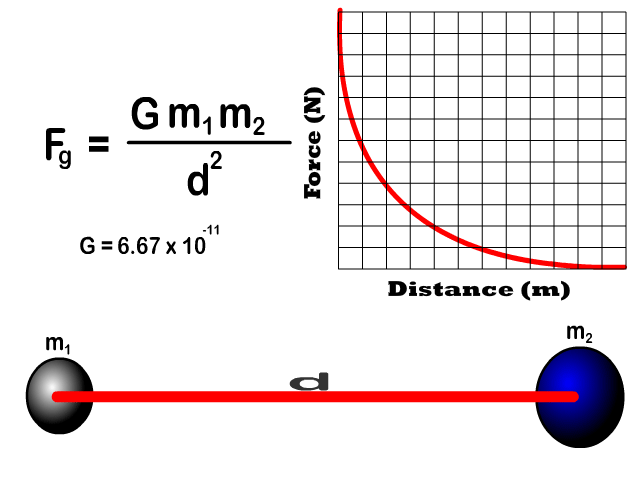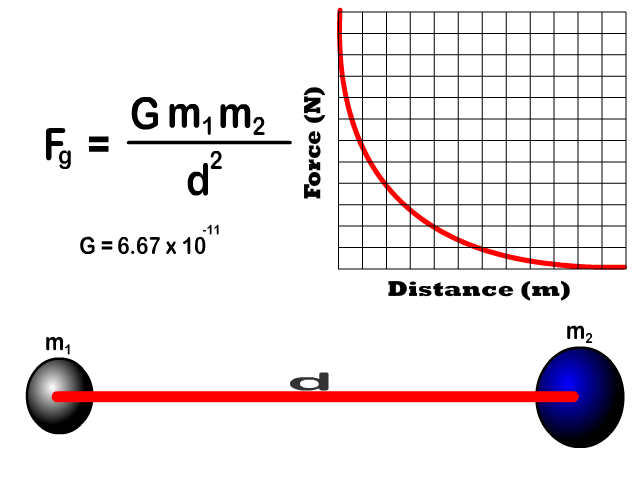
Key Concepts

This law is a cornerstone of classical mechanics. It applies universally — whether you're analyzing falling apples or orbiting satellites. Gravity is a long-range, central force that pulls masses together.

It’s an example of an inverse-square law: when distance doubles, gravitational force drops to a quarter. This mathematical pattern appears in electric forces, light intensity, and more.

Derivation of \( g = 9.8 \, \text{m/s}^2 \) from Universal Gravitation

The acceleration due to gravity \( g \) near the Earth's surface can be derived from Newton's Law of Universal Gravitation. This derivation connects the gravitational force between Earth and an object to the object's acceleration as it falls.

Step 1: Newton’s Law of Universal Gravitation

Newton’s Law states that the gravitational force \( F_g \) between two masses \( m_1 \) and \( m_2 \) separated by distance \( r \) is:

\[ F_g = G \frac{m_1 m_2}{r^2} \]

Here, \( G = 6.674 \times 10^{-11} \, \text{N} \cdot \text{m}^2/\text{kg}^2 \) is the universal gravitational constant.

Step 2: Force on an object near Earth's surface

Consider an object of mass \( m \) near the Earth's surface, and let Earth's mass be \( M_E \) and radius \( R_E \). The gravitational force pulling the object downward is:

\[ F_g = G \frac{M_E \cdot m}{R_E^2} \]

Since this force causes the object to accelerate downward, by Newton's second law:

\[ F_g = m \cdot g \]

Step 3: Equate the two expressions for \( F_g \)

Setting the gravitational force equal to the force from Newton's second law, we get:

\[ m \cdot g = G \frac{M_E \cdot m}{R_E^2} \]

We can cancel the object mass \( m \) on both sides since it is nonzero:

\[ g = G \frac{M_E}{R_E^2} \]

Step 4: Substitute known values

Using the known values for Earth's mass and radius:

Mass of Earth, \( M_E = 5.972 \times 10^{24} \, \text{kg} \)
Radius of Earth, \( R_E = 6.371 \times 10^6 \, \text{m} \)

Substitute into the formula:

\[ g = (6.674 \times 10^{-11}) \times \frac{5.972 \times 10^{24}}{(6.371 \times 10^{6})^2} \]

Step 5: Calculate \( g \)

Calculate the denominator:

\[ (6.371 \times 10^{6})^2 = 4.058 \times 10^{13} \]

Now, compute \( g \):

\[ g = (6.674 \times 10^{-11}) \times \frac{5.972 \times 10^{24}}{4.058 \times 10^{13}} = \frac{3.986 \times 10^{14}}{4.058 \times 10^{13}} = 9.82 \, \text{m/s}^2 \]

This matches the experimentally measured acceleration due to gravity near the Earth's surface.

Direction of Force

Gravity is always attractive and directed along the line connecting the two masses. Unlike electromagnetic forces, which can repel or attract, gravitational force has no repulsive counterpart.

Applications

Calculating planetary or satellite orbits
Predicting the motion of celestial bodies
Understanding tides and variations in gravitational field strength

Common Misconceptions

“Gravity only affects large objects.”
In reality, gravity acts between all objects with mass, regardless of size. The effect is just extremely weak at small scales.
“Gravity doesn’t act in space.”
In fact, space is full of gravitational interactions. Orbits, galaxies, and black holes are all governed by gravity.
“The Earth’s gravity stops at the atmosphere.”
Gravity extends infinitely — it just gets weaker with distance. Even astronauts in orbit are constantly falling toward Earth.
“Gravity is the same everywhere on Earth.”
Local variations in altitude, geology, and latitude affect the strength of gravity slightly.

Historical Context: Newton’s Discovery Story

The famous story goes that Sir Isaac Newton was inspired to formulate his theory of gravitation after seeing an apple fall from a tree. Sitting in his garden, he wondered why apples always fall straight down instead of sideways or upwards.

Newton realized the force pulling the apple downward might also be responsible for keeping the Moon in orbit around Earth. He reasoned that gravity must extend far beyond the Earth’s surface and that its strength decreases with distance.

By combining observation, mathematics, and physics, Newton formulated the inverse-square law of gravitation, unifying celestial and terrestrial mechanics into one universal law. This discovery revolutionized science and remains fundamental to physics today.

Example Calculation

What is the gravitational force between a 5 kg mass and a 1000 kg mass 2 meters apart?

\[ F = G \frac{(5)(1000)}{2^2} = (6.674 \times 10^{-11}) \cdot \frac{5000}{4} = 8.34 \times 10^{-8} \, \text{N} \]

Although tiny, this force is measurable with sensitive equipment and governs orbits of moons, planets, and satellites.

Formula	Use When	Notes
`F = mg`	Near Earth’s surface or similar large bodies	Assumes constant acceleration due to gravity; uniform field
\[ F = G \frac{m_1 m_2}{r^2} \]	Any two masses at any distance	Exact calculation of gravitational force using actual distance

Summary

Newton’s Law of Universal Gravitation states that every mass attracts every other mass with a force proportional to the product of their masses and inversely proportional to the square of the distance between them. This force is always attractive and acts over infinite distances. It underpins much of classical physics and astronomy, explaining motions from falling objects to planetary orbits.

Interactive Gravitational Force Simulator

Adjust masses and distance to see how the gravitational force changes.

Mass 1 (kg): Mass 2 (kg): Distance (m):