Potential Energy Curves
A Potential Energy Curve graphically shows how potential energy \( U(x) \) changes with respect to position \( x \). These curves help us predict motion, equilibrium points, and energy conservation in systems with conservative forces.
Understanding the Curve
- The vertical axis represents potential energy \( U(x) \).
- The horizontal axis represents position \( x \).
- Where the slope \( \frac{dU}{dx} \) is zero, the force is zero.
- A steeper slope implies a larger force, since \( F = -\frac{dU}{dx} \).
- Total energy \( E = U + K \) remains constant in conservative systems.

Solid line is potential energy.Dotted line is kinetic energy.
Key Formulas
Potential Energy Function:
\( U(x) \)
Force from Potential Energy:
\( F(x) = -\frac{dU}{dx} \)
(The force is the negative slope of the potential energy curve)
Change in Potential Energy:
\( \Delta U = -\int_{x_a}^{x_b} F(x) \, dx \)
This integral shows that the area under the force vs. position curve gives the change in potential energy (with a negative sign). This is especially useful when analyzing non-constant forces.
Worked Examples
Example 1: Using \( F(x) = -\frac{dU}{dx} \) to Find Force
Problem: Suppose the potential energy of a particle is given by:
\( U(x) = 3x^2 \) (in joules, with \( x \) in meters)
Find the expression for the force acting on the particle as a function of \( x \).
Solution:
We use the formula:
\( F(x) = -\frac{dU}{dx} \)
Take the derivative of \( U(x) \):
\( \frac{dU}{dx} = 6x \)
Then apply the negative sign:
\( F(x) = -6x \)
Answer: The force acting on the particle is \( F(x) = -6x \). This is a restoring force, like a spring!
Example 2: Using \( \Delta U = -\int_{x_a}^{x_b} F(x)\, dx \) to Find Change in Potential Energy
Problem: A particle experiences a force \( F(x) = 4x \) (in newtons). Calculate the change in potential energy as it moves from \( x = 1 \, \text{m} \) to \( x = 3 \, \text{m} \).
Solution:
Use the formula:
\( \Delta U = -\int_{1}^{3} 4x \, dx \)
First, compute the definite integral:
\( \int_{1}^{3} 4x \, dx = 4 \cdot \left[ \frac{x^2}{2} \right]_1^3 = 4 \cdot \left( \frac{9}{2} - \frac{1}{2} \right) = 4 \cdot 4 = 16 \)
Apply the negative sign:
\( \Delta U = -16 \, \text{J} \)
Answer: The potential energy decreased by 16 joules.
Equilibrium Points
Stable Equilibrium
A particle is in stable equilibrium when it sits at a local minimum of the potential energy curve. If the particle is slightly displaced, a restoring force pushes it back toward the equilibrium point.
At \( x = x_0 \), if \( \frac{dU}{dx} = 0 \) and \( \frac{d^2U}{dx^2} > 0 \), it's a stable equilibrium.
Example: A mass on a spring at the center of its motion — displacing it left or right results in a force pulling it back.
Unstable Equilibrium
A particle is in unstable equilibrium when it sits at a local maximum of the potential energy curve. Any small displacement leads to motion away from the point — it cannot return on its own.
At \( x = x_0 \), if \( \frac{dU}{dx} = 0 \) and \( \frac{d^2U}{dx^2} < 0 \), it's an unstable equilibrium.
Example: A pencil balanced on its tip — even a tiny disturbance causes it to fall over.
Looking at it Graphically
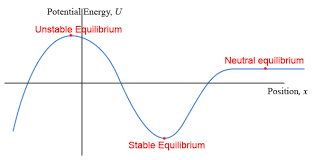
Looking at it Visually:
Interpreting the Curve
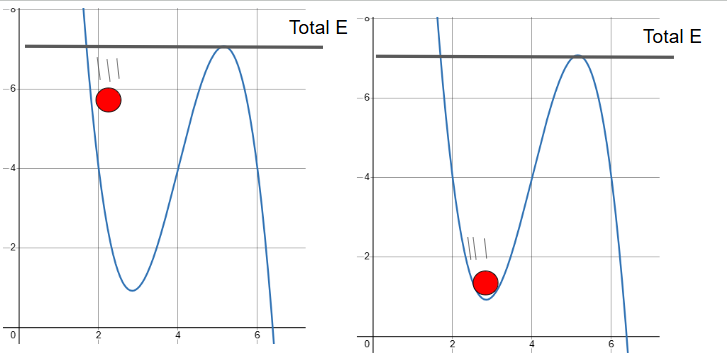
- Turning Points: Where total energy \( E \) intersects the potential curve \( U(x) \); here, kinetic energy is zero.
- Bound Motion: When the particle remains trapped between two turning points.
- Escape Energy: The minimum energy required to escape the potential well.
Example: Particle in a Potential Well
Consider a particle in a bowl-shaped potential energy curve. It moves back and forth between two turning points. When it reaches the bottom of the well (minimum \( U \)), it has maximum kinetic energy. At the edges (where \( E = U \)), it momentarily stops.

Types of Potential Energy Curves
- Harmonic Potential: \( U(x) = \frac{1}{2}kx^2 \) (spring systems)
- Gravitational Potential: \( U(y) = mgy \)
- Electric Potential (covered in E & M): \( U(r) = k\frac{q_1q_2}{r} \)
Total Energy and Motion
In a conservative system:
- Total Energy \( E \) is constant.
- At any point: \( E = U(x) + K(x) \).
- Where \( U(x) = E \), kinetic energy is zero (turning point).
- If \( U(x) > E \), motion is not allowed (classically forbidden region).
Kinetic Energy from Potential:
\( K(x) = E - U(x) \)
Applications
- Analyzing oscillatory systems (springs, pendulums)
- Predicting stability of equilibrium points in mechanical systems
- Understanding escape velocities in orbital mechanics
- Modeling atomic and molecular interactions in chemistry and quantum physics
Answer: Only where \( U(x) \leq E \)
Challenge Questions
- If a particle starts at rest at a local maximum of \( U(x) \), what will happen?
- How do you determine the direction of force from the graph?
- Can a particle move through a point where \( U(x) > E \)? Why or why not?
Watch this video for a better understanding of potential energy curves:
Watch this video for a visual demonstration of potential energy curves:
Conclusion
Potential energy curves provide deep insight into the motion of objects under conservative forces. By analyzing the shape of the curve and total mechanical energy, we can determine motion, equilibrium, and system behavior.