← Back to Concepts

Restoring Forces and Conditions for SHM

Oscillations arise when an object is subject to a force that acts to restore it to an equilibrium position. This type of force is called a restoring force.

Definition

A restoring force is a force that is always directed toward the system's equilibrium position and is proportional to the displacement from that position.

$$F = -kx$$

This is known as Hooke's Law, and it describes the restoring force in an ideal mass-spring system. The negative sign indicates that the force is directed opposite the displacement.

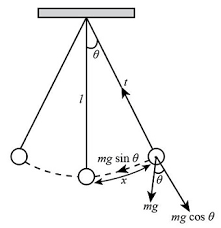
Pendulum as a Restoring Force System

A simple pendulum provides another excellent example of a restoring force system. When a pendulum is displaced from its equilibrium position, gravity creates a restoring force that brings it back.

$$F = -mg \sin(\theta)$$

Where:

$F$ is the restoring force
$m$ is the mass of the pendulum bob
$g$ is the acceleration due to gravity
$\theta$ is the angular displacement from equilibrium

For small angles ($\theta < 15°$), we can approximate $\sin(\theta) \approx \theta$, giving us:

$$F \approx -mg\theta$$

This shows that the restoring force is proportional to the displacement (angle), which is the key characteristic of simple harmonic motion.

Mathematical Form of SHM for Pendulum

For a simple pendulum, we can derive the mathematical form of simple harmonic motion. The restoring force component along the arc of motion is:

$$F = -mg \sin(\theta)$$

For small angles, $\sin(\theta) \approx \theta$, so:

$$F \approx -mg\theta$$

The displacement along the arc is $s = L\theta$, where $L$ is the length of the pendulum. Therefore:

$$\theta = \frac{s}{L}$$

Substituting this into the force equation:

$$F \approx -mg\frac{s}{L} = -\frac{mg}{L}s$$

This has the form $F = -ks$ where $k = \frac{mg}{L}$. Using Newton's Second Law:

$$m\frac{d^2s}{dt^2} = -\frac{mg}{L}s$$

Which simplifies to:

$$\frac{d^2s}{dt^2} = -\frac{g}{L}s$$

Defining $\omega = \sqrt{\frac{g}{L}}$, we get:

$$\frac{d^2s}{dt^2} = -\omega^2 s$$

This is the same form as the spring oscillator, confirming that a pendulum exhibits simple harmonic motion for small angles.

Figure 1: A spring exerts a restoring force directed toward equilibrium.

Mathematical Form of SHM for Spring-Block Oscillator

Combining Hooke's Law with Newton's Second Law gives:

$$m\frac{d^2x}{dt^2} = -kx$$

Which simplifies to:

$$\frac{d^2x}{dt^2} = -\frac{k}{m}x$$

Defining $\omega = \sqrt{\frac{k}{m}}$, we write:

$$\frac{d^2x}{dt^2} = -\omega^2 x$$

This differential equation defines SHM: the acceleration is proportional to and opposite the displacement.

Figure: Acceleration in SHM increases with displacement and always points toward equilibrium.

Key Characteristics

The force is proportional to displacement: more displacement → stronger force.
The force acts in the opposite direction of displacement.
These two conditions lead to simple harmonic motion (SHM).

Summary of SHM Conditions

The net force is proportional to the displacement: $F = -kx$
The motion follows $\frac{d^2x}{dt^2} = -\omega^2 x$
The system exhibits sinusoidal oscillations (if undamped)

Spring-Block Oscillator Simulation

Mass (kg): 1.0 Spring Constant (N/m): 10

Angular Frequency (ω): 3.16 rad/s

Pendulum Simulation

Explore how the pendulum's motion depends on its length, mass, and initial displacement:

Length (m): 1.0 Mass (kg): 1.0 Amplitude (deg): 20

Angular Frequency (ω): 3.13 rad/s | Period (T): 2.01 s