Shell Theorem
The Shell Theorem, formulated by Isaac Newton, describes how spherical mass distributions affect the gravitational field. It is particularly important in understanding gravitational interactions inside and outside uniform spheres like planets and stars.
The Two Main Results of the Shell Theorem
- Outside a uniform spherical shell: The gravitational force acts as if all the mass were concentrated at the center.
- Inside a uniform spherical shell: The net gravitational force at any point inside is zero.
Gravitational Force Outside the Shell
If a point mass \( m \) is located a distance \( r \) from the center of a uniform spherical shell (or solid sphere) of mass \( M \), and \( r \geq R \) (outside the shell), then:
This is identical to the force from a point mass located at the center of the sphere.
Gravitational Force Inside the Shell
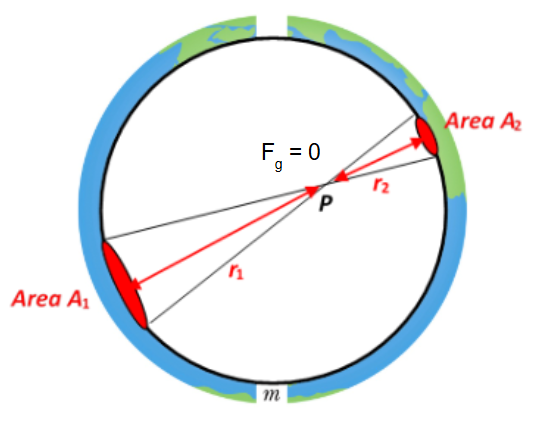
If the point mass is located inside a uniform spherical shell (i.e., \( r < R \)), the shell’s gravitational pull cancels out symmetrically in all directions:
Thus, the shell exerts no net gravitational force on the object inside it.
Applications of Shell Theorem
- Justifies treating planets as point masses in orbital calculations
- Important in gravitational field mapping and geophysics
- Used in cosmology to study spherically symmetric mass distributions
Summary:
The Shell Theorem is essential for simplifying gravitational calculations involving spheres and helps explain many real-world and astronomical phenomena with elegant precision.