← Back to Concepts

SHM Systems

There are several physical systems that exhibit simple harmonic motion (SHM) under specific conditions. Understanding these systems helps us apply SHM equations and analyze real-world oscillations.

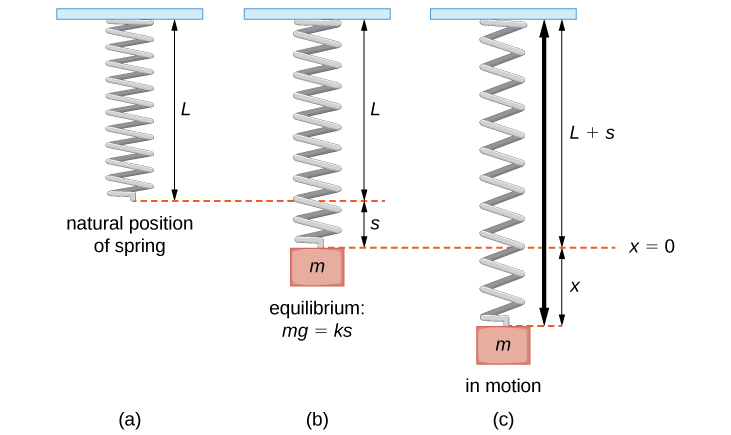
1. Horizontal and Vertical Spring-Mass Systems

In these systems, a mass is attached to a spring either on a frictionless horizontal surface or hanging vertically under gravity. Both setups can undergo SHM if the restoring force is proportional to displacement from equilibrium:

\( F = -kx \quad \Rightarrow \quad a = -\frac{k}{m}x \)

This leads to motion described by the differential equation for SHM:

\( \frac{d^2x}{dt^2} = -\omega^2 x \quad \text{where} \quad \omega = \sqrt{\frac{k}{m}} \)

For vertical systems, the gravitational force shifts the equilibrium point but doesn’t affect the oscillatory motion as long as we measure displacement from the new equilibrium.

Figure: A block on a spring moving in SHM. Vertical systems oscillate around a shifted equilibrium.

Watch this video for better understanding:

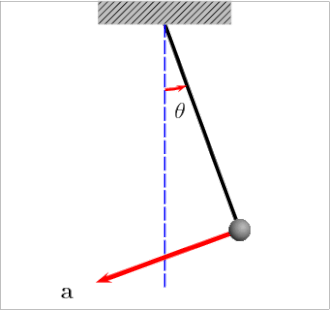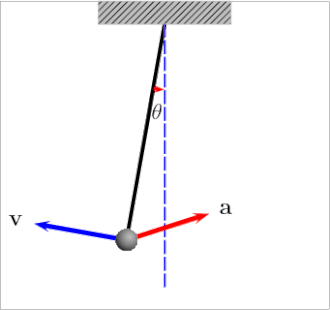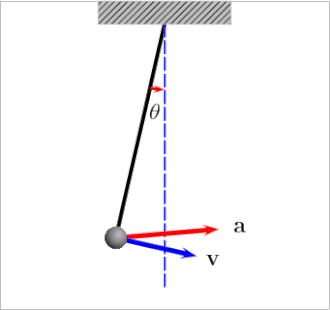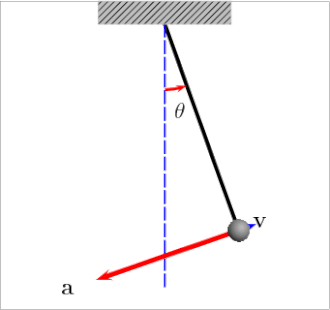
2. Simple Pendulum (for small angles)

A simple pendulum is a mass hanging from a string of fixed length. When displaced by a small angle and released, it oscillates back and forth due to the component of gravity acting as a restoring force.

The restoring torque leads to SHM only when the angle is small (\( \theta \lesssim 15^\circ \)), so the approximation \( \sin\theta \approx \theta \) holds true.

\( \frac{d^2\theta}{dt^2} = -\frac{g}{L} \theta \quad \Rightarrow \quad \omega = \sqrt{\frac{g}{L}} \)

Figure: At small angles, the pendulum approximates SHM.

Summary of Common SHM Systems

Horizontal Spring: Ideal SHM when friction is negligible.
Vertical Spring: SHM about new equilibrium point under gravity.
Pendulum: SHM if angle is small enough for \( \sin\theta \approx \theta \).

These ideal systems help us explore SHM concepts, predict motion, and connect theory to experimental setups.